题目内容
已知点M(-2,0),N(2,0),动点P满足条件|PM|-|PN|=2| 2 |
(Ⅰ)求W的方程;
(Ⅱ)若A,B是W上的不同两点,O是坐标原点,求
| OA |
| OB |
分析:(Ⅰ)依题意,点P的轨迹是以M,N为焦点的双曲线的右支,由此能求出其方程.
(Ⅱ)当直线AB的斜率不存在时,设直线AB的方程为x=x0,此时A(x0,
(2)),B(x0,-
),
•
=2,当直线AB的斜率存在时,设直线AB的方程为y=kx+b,代入双曲线方程
-
=1中,得(1-k2)x2-2kbx-b2-2=0.依题意可知方程有两个不相等的正数根,由此入手能求出
•
的最小值.
(Ⅱ)当直线AB的斜率不存在时,设直线AB的方程为x=x0,此时A(x0,
|
|
| OA |
| OB |
| x2 |
| 2 |
| y2 |
| 2 |
| OA |
| OB |
解答:解:(Ⅰ)依题意,点P的轨迹是以M,N为焦点的双曲线的右支,
所求方程为:
-
=1(x>0)
(Ⅱ)当直线AB的斜率不存在时,设直线AB的方程为x=x0,
此时A(x0,
),
B(x0,-
),
•
=2
当直线AB的斜率存在时,设直线AB的方程为y=kx+b,
代入双曲线方程
-
=1中,得:
(1-k2)x2-2kbx-b2-2=01°
依题意可知方程1°有两个不相等的正数根,设A(x1,y1),B(x2,y2),
则
,
解得|k|>1又
•
=x1x2+y1y2
=x1x2+(kx1+b)(kx2+b)
=(1+k2)x1x2+kb(x1+x2)+b2
=
=2+
>2
综上可知
•
的最小值为2.
所求方程为:
| x2 |
| 2 |
| y2 |
| 2 |
(Ⅱ)当直线AB的斜率不存在时,设直线AB的方程为x=x0,
此时A(x0,
|
B(x0,-
|
| OA |
| OB |
当直线AB的斜率存在时,设直线AB的方程为y=kx+b,
代入双曲线方程
| x2 |
| 2 |
| y2 |
| 2 |
(1-k2)x2-2kbx-b2-2=01°
依题意可知方程1°有两个不相等的正数根,设A(x1,y1),B(x2,y2),
则
|
解得|k|>1又
| OA |
| OB |
=x1x2+(kx1+b)(kx2+b)
=(1+k2)x1x2+kb(x1+x2)+b2
=
| 2k2+2 |
| k2-1 |
| 4 |
| k2-1 |
综上可知
| OA |
| OB |
点评:本题考查双曲线的性质和应用,解题时要认真审题,仔细解答,注意公式的合理运用.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
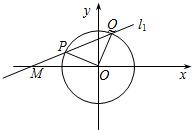 已知点M(-2,0),⊙O:x2+y2=1(如图);若过点M的直线l1交圆于P、Q两点,且圆孤PQ恰为圆周的
已知点M(-2,0),⊙O:x2+y2=1(如图);若过点M的直线l1交圆于P、Q两点,且圆孤PQ恰为圆周的