题目内容
【题目】已知函数
=2cos（ωx
）（ω>0）满足：f（
）=f（
），且在区间（，）内有最大值但没有最小值，给出下列四个命题：P1：在[0，2π]上单调递减；P2：的最小正周期是4π；P3：的图象关于直线x
对称；P4：的图象关于点（
，0）对称.其中的真命题是( )
A.P1，P2B.P2，P4C.P1，P3D.P3，P4
【答案】B
【解析】
根据对称性和最值求出函数解析式，即可判定单调性，周期和对称性.
函数
=2cos（ωx
）（ω>0）满足：f（
）=f（
），
即对称轴
，
且在区间（，）内有最大值但没有最小值，
，且
，
即
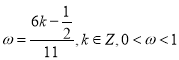，所以
，
所以
，
对于P1：
，所以在[0，2π]上不单调，P1不是真命题；
P2：的最小正周期是
4π，P2是真命题；
P3：
不是最值，的图象不关于直线x
对称，P3不是真命题；
P4：
，的图象关于点（
，0）对称，P4是真命题.
故选：B
【题目】某校为了了解学生对消防知识的了解情况，从高一年级和高二年级各选取100名同学进行消防知识竞赛.下图（1）和图（2）分别是对高一年级和高二年级参加竞赛的学生成绩按
分组，得到的频率分布直方图.
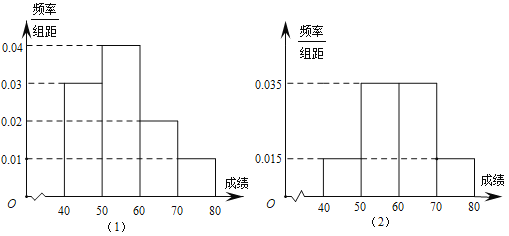
（1）请计算高一年级和高二年级成绩小于60分的人数；
（2）完成下面
列联表，并回答：有多大的把握可以认为“学生所在的年级与消防常识的了解存在相关性”？
成绩小于60分人数 | 成绩不小于60分人数 | 合计 | |
高一 | |||
高二 | |||
合计 |
附：临界值表及参考公式：
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某公司近年来科研费用支出
万元与公司所获得利润
万元之间有如下的统计数据：
x | 2 | 3 | 4 | 5 |
Y | 18 | 27 | 32 | 35 |
（1）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程
；
（2）试根据（1）求出的线性回归方程，预测该公司科研费用支出为10万元时公司所获得的利润．
参考公式：用最小二乘法求线性回归方程的系数公式：
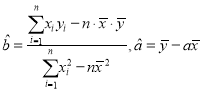
参考数据：2×18+3×27+4×32+5×35=420
【题目】某蛋糕店制作并销售一款蛋糕，制作一个蛋糕成本3元，且以8元的价格出售，若当天卖不完，剩下的则无偿捐献给饲料加工厂。根据以往100天的资料统计，得到如下需求量表。该蛋糕店一天制作了这款蛋糕
个，以
（单位：个，
，
）表示当天的市场需求量，
（单位：元）表示当天出售这款蛋糕获得的利润.
需求量/个 |
|
|
|
|
|
天数 | 15 | 25 | 30 | 20 | 10 |
（1）当
时，若
时获得的利润为
，
时获得的利润为
，试比较和的大小；
（2）当时，根据上表，从利润不少于570元的天数中，按需求量分层抽样抽取6天.
（i）求此时利润关于市场需求量的函数解析式，并求这6天中利润为650元的天数；
（ii）再从这6天中抽取3天做进一步分析，设这3天中利润为650元的天数为
，求随机变量的分布列及数学期望.
