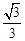题目内容
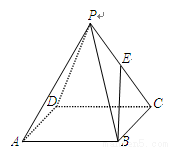
如图,正四棱锥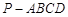 的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( )
的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( )
A.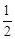 B.
B.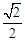
C.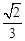 D.
D.
【答案】
D
【解析】
试题分析:由于正四棱锥 的所有棱长相等,设为2,BE=
的所有棱长相等,设为2,BE= ,,EO=1,OB=
,,EO=1,OB= ,E为PC的中点,那么可知连接AC,BD的交点O,则将BE平移到PA,则在三角形EOB中,利用三边长度可知异面直线BE与PA所成角的余弦值是
,E为PC的中点,那么可知连接AC,BD的交点O,则将BE平移到PA,则在三角形EOB中,利用三边长度可知异面直线BE与PA所成角的余弦值是 ,故选D.
,故选D.
考点:异面直线所成的角的求解
点评:求解异面直线的所成的角,一般采用平移法,放在一个三角形中来求解运算,属于基础题。

练习册系列答案
相关题目
 一个正四棱锥的所有棱长均为2,其俯视图如图所示,则该正四棱锥的正视图的面积为
一个正四棱锥的所有棱长均为2,其俯视图如图所示,则该正四棱锥的正视图的面积为 如图,正四棱锥P-ABCD的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( )
如图,正四棱锥P-ABCD的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( ) (2012•丰台区二模)一个正四棱锥的所有棱长均为2,其俯视图如图所示,则该正四棱锥的正视图的面积为( )
(2012•丰台区二模)一个正四棱锥的所有棱长均为2,其俯视图如图所示,则该正四棱锥的正视图的面积为( )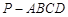 的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是
的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是 B.
B.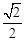 C.
C.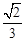 D.
D.