题目内容
已知
，那么函数y=x2+x+1（ ）A．有最小值
，没有最大值B．有最小值
，有最大值1C．有最小值1，有最大值
D．有最小值
，有最大值
【答案】分析：先把函数y=x2+x+1配方，找到对称轴和区间的关系；再根据开口向上的二次函数离对称轴越远，函数值越大这一结论即可求解．
解答：解：因为y=x2+x+1=
在[-
，
]上递增，在[-1，-
]上递减．
且
离对称轴远．
所以当x=
时有最大值y=
+
+1=
；
当x=-
时有最小值y=
．
故选：D．
点评：本题主要考查求二次函数在闭区间上的最值问题．开口向上的二次函数离对称轴越远，函数值越大；开口向下的二次函数离对称轴越远，函数值越小．
解答：解：因为y=x2+x+1=
在[-
，]上递增，在[-1，-]上递减．且
离对称轴远．所以当x=
时有最大值y=++1=；当x=-
时有最小值y=．故选：D．
点评：本题主要考查求二次函数在闭区间上的最值问题．开口向上的二次函数离对称轴越远，函数值越大；开口向下的二次函数离对称轴越远，函数值越小．
练习册系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
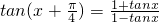
，那么函数y＝tanx的周期为π．类比可推出：已知x∈R且
，那么函数y＝f(x)的周期是
，那么函数y=tanx的周期为π．类比可推出：已知x∈R且
，那么函数y=f（x）的周期是
，那么函数y=tanx的周期为π．类比可推出：已知x∈R且
，那么函数y=f（x）的周期是（ ）
，那么函数y=x2+x+1
，没有最大值