题目内容
已知函数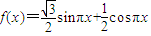 ,x∈R.
,x∈R.(Ⅰ)求函数f(x)的最大值和最小值;
(Ⅱ)如图,函数f(x)在[-1,1]上的图象与x轴的交点从左到右分别为M、N,图象的最高点为P,求
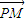 与
与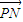 的夹角的余弦.
的夹角的余弦.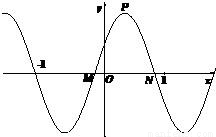
【答案】分析:(Ⅰ)利用两角和的正弦函数化简函数的表达式,然后求函数f(x)的最大值和最小值;
(Ⅱ)解法一:通过函数为0,求出M,N的坐标,确定P的位置,求出 与
与 ,求出
,求出 与
与 的夹角的余弦.
的夹角的余弦.
解法二:过点P作PA⊥x轴于A,则|PA|=1,求出|PM|,|PN|在三角形中利用余弦定理求出 与
与 的夹角的余弦.
的夹角的余弦.
解法三:过点P作PA⊥x轴于A,则|PA|=1,在Rt△PAM中,求出 ,通过二倍角公式求出
,通过二倍角公式求出 与
与 的夹角的余弦.
的夹角的余弦.
解答: 解:(Ⅰ)∵
解:(Ⅰ)∵
= (2分)
(2分)
∵x∈R∴ ,
,
∴函数f(x)的最大值和最小值分别为1,-1.(4分)
(Ⅱ)解法1:令 得
得 ,
,
∵x∈[-1,1]∴ 或
或 ∴
∴ ,(6分)
,(6分)
由 ,且x∈[-1,1]得
,且x∈[-1,1]得 ∴
∴ ,(8分)
,(8分)
∴ ,(10分)
,(10分)
∴ =
= .(12分)
.(12分)
解法2:过点P作PA⊥x轴于A,则|PA|=1,
由三角函数的性质知 ,(6分)
,(6分) ,(8分)
,(8分)
由余弦定理得 (10分)
(10分)
= .(12分)
.(12分)
解法3:过点P作PA⊥x轴于A,则|PA|=1,
由三角函数的性质知 ,(6分)
,(6分) (8分)
(8分)
在Rt△PAM中, (10分)
(10分)
∵PA平分∠MPN∴cos∠MPN=cos2∠MPA=2cos2∠MPA-1= .(12分)
.(12分)
点评:本题是中档题,考查三角函数的化简求值,向量的夹角的求法,可以通过向量的数量积解决,也可以通过三角形解决,考查计算能力,常考题型.
(Ⅱ)解法一:通过函数为0,求出M,N的坐标,确定P的位置,求出
 与
与 ,求出
,求出 与
与 的夹角的余弦.
的夹角的余弦.解法二:过点P作PA⊥x轴于A,则|PA|=1,求出|PM|,|PN|在三角形中利用余弦定理求出
 与
与 的夹角的余弦.
的夹角的余弦.解法三:过点P作PA⊥x轴于A,则|PA|=1,在Rt△PAM中,求出
 ,通过二倍角公式求出
,通过二倍角公式求出 与
与 的夹角的余弦.
的夹角的余弦.解答:
 解:(Ⅰ)∵
解:(Ⅰ)∵
=
 (2分)
(2分)∵x∈R∴
 ,
,∴函数f(x)的最大值和最小值分别为1,-1.(4分)
(Ⅱ)解法1:令
 得
得 ,
,∵x∈[-1,1]∴
 或
或 ∴
∴ ,(6分)
,(6分)由
 ,且x∈[-1,1]得
,且x∈[-1,1]得 ∴
∴ ,(8分)
,(8分)∴
 ,(10分)
,(10分)∴
 =
= .(12分)
.(12分)解法2:过点P作PA⊥x轴于A,则|PA|=1,
由三角函数的性质知
 ,(6分)
,(6分) ,(8分)
,(8分)由余弦定理得
 (10分)
(10分)=
 .(12分)
.(12分)解法3:过点P作PA⊥x轴于A,则|PA|=1,
由三角函数的性质知
 ,(6分)
,(6分) (8分)
(8分)在Rt△PAM中,
 (10分)
(10分)∵PA平分∠MPN∴cos∠MPN=cos2∠MPA=2cos2∠MPA-1=
 .(12分)
.(12分)点评:本题是中档题,考查三角函数的化简求值,向量的夹角的求法,可以通过向量的数量积解决,也可以通过三角形解决,考查计算能力,常考题型.

练习册系列答案
相关题目
 (x∈R).若
(x∈R).若 ,
, .求cos2x的值.
.求cos2x的值. ,x∈R,且
,x∈R,且
 ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值.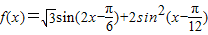 (x∈R).
(x∈R). ,x∈R
,x∈R
 ,x∈R,且
,x∈R,且
 ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值.