题目内容
已知F1(-1,0),F2(1,0),点p满足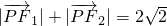 ,记点P的轨迹为E.
,记点P的轨迹为E.
(Ⅰ)求轨迹E的方程;
(Ⅱ)过点F2(1,0)作直线l与轨迹E交于不同的两点A、B,设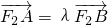 ,T(2,0),,若λ∈[-2,-1],求
,T(2,0),,若λ∈[-2,-1],求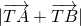 的取值范围.
的取值范围.
解:(Ⅰ)由 知,点P的轨迹为以F1,F2为焦点,长轴长为
知,点P的轨迹为以F1,F2为焦点,长轴长为 的椭圆
的椭圆
所以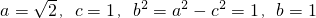
轨迹方程为 .
.
(Ⅱ)根据题设条件可设直线l的方程为x=ky+1,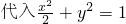 中,得(k2+2)y2+2ky-1=0.
中,得(k2+2)y2+2ky-1=0.
设A(x1,y1),B(x2,y2),
则由根与系数的关系得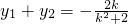 ①
①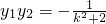 .②
.②
∵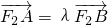 ,∴有
,∴有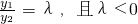 .
.
将①式平方除以②式,得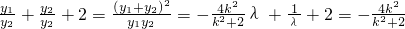
由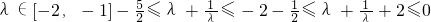

∵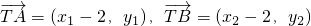 ,∴
,∴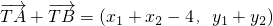 .
.
又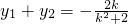 ,∴
,∴ .
.
故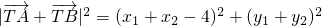 =
= =
=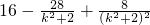
令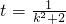 .∵
.∵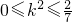 ∴
∴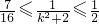 ,即
,即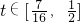 .
.
∴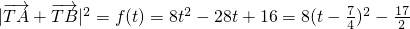 .
.
而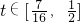 ,∴
,∴ .
.
∴ .
.
分析:(Ⅰ)由 知,点P的轨迹为以F1,F2为焦点,长轴长为
知,点P的轨迹为以F1,F2为焦点,长轴长为 的椭圆,由此能求出其轨迹方程.
的椭圆,由此能求出其轨迹方程.
(Ⅱ)根据题设条件可设直线l的方程为x=ky+1,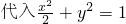 中,得(k2+2)y2+2ky-1=0.设A(x1,y1),B(x2,y2),则
中,得(k2+2)y2+2ky-1=0.设A(x1,y1),B(x2,y2),则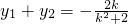 ,
,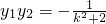 .由
.由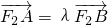 ,知有
,知有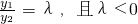 .所以
.所以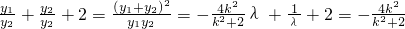 ,由
,由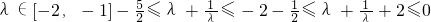
 .由此能求出
.由此能求出 .
.
点评:本题考查轨迹方程的求法,求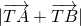 的取值范围.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
的取值范围.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
 知,点P的轨迹为以F1,F2为焦点,长轴长为
知,点P的轨迹为以F1,F2为焦点,长轴长为 的椭圆
的椭圆所以
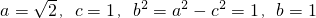
轨迹方程为
 .
.(Ⅱ)根据题设条件可设直线l的方程为x=ky+1,
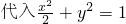 中,得(k2+2)y2+2ky-1=0.
中,得(k2+2)y2+2ky-1=0.设A(x1,y1),B(x2,y2),
则由根与系数的关系得
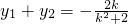 ①
①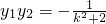 .②
.②∵
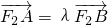 ,∴有
,∴有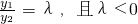 .
.将①式平方除以②式,得
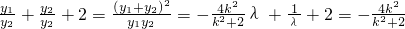
由
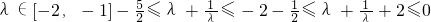

∵
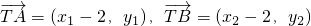 ,∴
,∴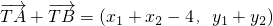 .
.又
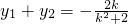 ,∴
,∴ .
.故
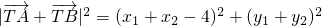 =
= =
=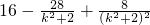
令
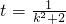 .∵
.∵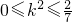 ∴
∴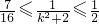 ,即
,即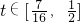 .
.∴
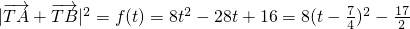 .
.而
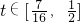 ,∴
,∴ .
.∴
 .
.分析:(Ⅰ)由
 知,点P的轨迹为以F1,F2为焦点,长轴长为
知,点P的轨迹为以F1,F2为焦点,长轴长为 的椭圆,由此能求出其轨迹方程.
的椭圆,由此能求出其轨迹方程.(Ⅱ)根据题设条件可设直线l的方程为x=ky+1,
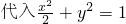 中,得(k2+2)y2+2ky-1=0.设A(x1,y1),B(x2,y2),则
中,得(k2+2)y2+2ky-1=0.设A(x1,y1),B(x2,y2),则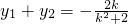 ,
,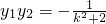 .由
.由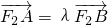 ,知有
,知有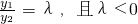 .所以
.所以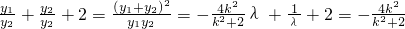 ,由
,由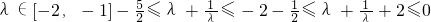
 .由此能求出
.由此能求出 .
.点评:本题考查轨迹方程的求法,求
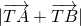 的取值范围.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
的取值范围.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化. 
练习册系列答案
相关题目