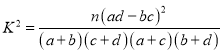题目内容
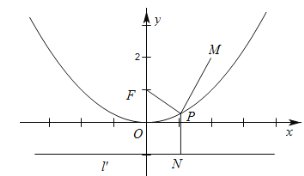
【题目】抛物线![]() 的焦点为F,P为其上一动点,设直线l与抛物线C相交于A,B两点,点
的焦点为F,P为其上一动点,设直线l与抛物线C相交于A,B两点,点![]() 下列结论正确的是( )
下列结论正确的是( )
A.|PM| +|PF|的最小值为3
B.抛物线C上的动点到点![]() 的距离最小值为3
的距离最小值为3
C.存在直线l,使得A,B两点关于![]() 对称
对称
D.若过A、B的抛物线的两条切线交准线于点T,则A、B两点的纵坐标之和最小值为2
【答案】AD
【解析】
根据抛物线的性质对每个命题进行判断.
A.设![]() 是抛物线的准线,过
是抛物线的准线,过![]() 作
作![]() 于
于![]() ,则
,则![]() ,当且仅当
,当且仅当![]() 三点共线时等号成立.所以
三点共线时等号成立.所以![]() 最小值是3,A正确;
最小值是3,A正确;
B.设![]() 是抛物线上任一点,即
是抛物线上任一点,即![]() ,
,![]() ,
,![]() 时,
时,![]() ,B错误;
,B错误;
C.假设存在直线![]() ,使得A,B两点关于
,使得A,B两点关于![]() 对称,设
对称,设![]() 方程为
方程为![]() ,由
,由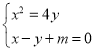 得
得![]() ,
,
所以![]() ,
,![]() ,设
,设![]() ,则
,则![]() ,
,![]() 中点为
中点为![]() ,则
,则![]() ,
,![]() ,
,![]() 必在直线
必在直线![]() 上,
上,
所以![]() ,
,![]() ,这与直线
,这与直线![]() 抛物线相交于两个点矛盾,故不存在,C错误;
抛物线相交于两个点矛盾,故不存在,C错误;
D.设![]() ,由
,由![]() 即
即![]() ,得
,得![]() ,则切线
,则切线![]() 方程为
方程为![]() ,
,
即![]() ,同理
,同理![]() 方程是
方程是![]() ,
,
由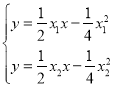 ,解得
,解得 ,由题意
,由题意![]() 在准线
在准线![]() 上,
上,
所以![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() 时,
时,![]() 为最小值.D正确.
为最小值.D正确.
故选:AD.

练习册系列答案
相关题目