题目内容
设函数![]()
(I)求证函数![]() 有两个零点;
有两个零点;
(II)设x1,x2是函数![]() 的两个零点,求| x1-x2|的范围;
的两个零点,求| x1-x2|的范围;
(III)求证函数![]() 的零点x1,x2至少有一个在区间(0,2)内.
的零点x1,x2至少有一个在区间(0,2)内.
(I)证明:![]()
![]()

又![]()
故函数![]() 有两个零点
有两个零点
(II)若![]() 的两个零点,
的两个零点,
则![]() 的两根
的两根
![]()

故![]()
(III)![]()
由(I)知![]()
![]()
(i)当![]()
又![]()
![]() 在区间(0,1)内至少有一个零点
在区间(0,1)内至少有一个零点
(ii)当![]()
![]()
![]() 在区间(1,2)内有一零点,
在区间(1,2)内有一零点,
综合(i)(ii),可知函数![]() 在区间(0,2)内至少有一个零点.
在区间(0,2)内至少有一个零点.

练习册系列答案
相关题目
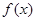 构成的集合:“①方程
构成的集合:“①方程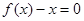 有实数根;②函数
有实数根;②函数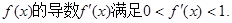 ”
”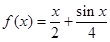 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由; 成立。试用这一性质证明:方程
成立。试用这一性质证明:方程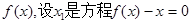 的实数根,求证:对于
的实数根,求证:对于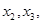 当
当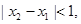 且
且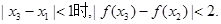
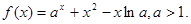
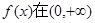 上单调递增;
上单调递增;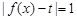 有三个不同的实根,求t的值;
有三个不同的实根,求t的值;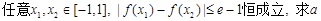 的取值范围。
的取值范围。