Question

已知椭圆经过点和点（，1），求椭圆的标准方程.

Answer 1

解法一：设椭圆的方程为mx²+ny²=1(m＞0,n＞0).

∵点和点都在椭圆上,

∴

∴

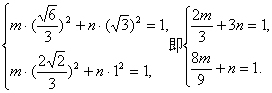
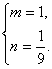
∴所求椭圆的标准方程为.

解法二：当椭圆的焦点在x轴上时，设椭圆的方程为(a＞b＞0).

∵点和点在椭圆上，

∴

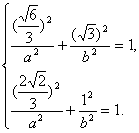
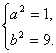∴而a＞b＞0,

∴a²=1,b²=9不合题意,

即焦点在x轴上的椭圆的方程不存在.

当椭圆的焦点在y轴上时，设椭圆的标准方程为(a＞b＞0).

∵点和点在椭圆上，

∴∴

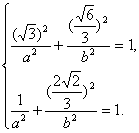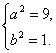
∴所求椭圆的方程为+x²=1.

绿色通道：

通过本例看出，已知椭圆经过两点，求椭圆的标准方程时，把椭圆的方程设成mx²+ny²=1的形式有两个优点：①列出的方程组中分母不含字母；②不用讨论焦点所在的坐标轴.