题目内容
已知双曲线
-
=1(a>0,b>0)的两条渐近线均和圆C:x2+y2-6x+5=0相切,则此双曲线的离心率为 ; 又若双曲线的焦点到渐近线的距离为2,则此双曲线的方程为 .
| x2 |
| a2 |
| y2 |
| b2 |
考点:双曲线的简单性质
专题:计算题,作图题,圆锥曲线的定义、性质与方程
分析:由题意,圆C:x2+y2-6x+5=0的方程可化为(x-3)2+y2=4;从而可得故
=
;从而求离心率;再由双曲线的焦点到渐近线的距离为2可得b=2;从而求方程.
| b |
| a |
| 2 | ||
|
解答:
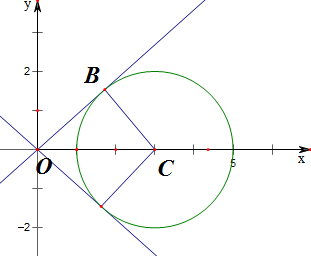 解:由题意,圆C:x2+y2-6x+5=0的方程可化为
解:由题意,圆C:x2+y2-6x+5=0的方程可化为
(x-3)2+y2=4;
故OC=3,BC=2,OB=
;
故
=
;
故e=
=
=
;
设双曲线的焦点为(c,0);
其一条渐近线方程为
+
=0,
即bx+ay=0;
故双曲线的焦点到渐近线的距离d=
=b=2;
故a=
;故此双曲线的方程为
-
=1;
故答案为:
;
-
=1.
 解:由题意,圆C:x2+y2-6x+5=0的方程可化为
解:由题意,圆C:x2+y2-6x+5=0的方程可化为(x-3)2+y2=4;
故OC=3,BC=2,OB=
| 5 |
故
| b |
| a |
| 2 | ||
|
故e=
| c |
| a |
1+(
|
3
| ||
| 5 |
设双曲线的焦点为(c,0);
其一条渐近线方程为
| x |
| a |
| y |
| b |
即bx+ay=0;
故双曲线的焦点到渐近线的距离d=
| |bc| | ||
|
故a=
| 5 |
| x2 |
| 5 |
| y2 |
| 4 |
故答案为:
3
| ||
| 5 |
| x2 |
| 5 |
| y2 |
| 4 |
点评:本题考查了双曲线的定义及性质应用,属于基础题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
已知双曲线C以直线x±2y=0为渐近线,且经过点A(2,-2),则双曲线C的方程是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列各点在方程x2-xy+2y+1=0表示的曲线上的是( )
| A、(0,0) |
| B、(1,1) |
| C、(1,-1) |
| D、(1,-2) |
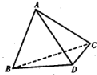 四面体ABCD中,△ABC是正三角形,△BCD是等腰直角三角形,其中BD=DC=
四面体ABCD中,△ABC是正三角形,△BCD是等腰直角三角形,其中BD=DC=