题目内容
在△ABC中,若AB=1,BC=2,则角C的取值范围是
- A.0<C≤

- B.0<C<

- C.
 <C<
<C<
- D.
 <C≤
<C≤
A
分析:利用两边之和大于第三边,两边之差小于第三边可求得b的范围,进而利用余弦定理表示出cosC的表达式,根据b的范围求得cosC的范围,进而求得C的范围.
解答:因为c=AB=1,a=BC=2,b=AC
根据两边之和大于第三边,两边之差小于第三边可知
1<b<3,根据余弦定理
cosC= (a2+b2-c2)
(a2+b2-c2)
= (4+b2-1)
(4+b2-1)
= (3+b2)
(3+b2)
= +
+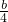
= (
( -
- )2+
)2+ ≥
≥
所以0<C≤30°
故选A
点评:本题主要考查了解三角形问题.考查了学生分析问题的基本的推理能力.
分析:利用两边之和大于第三边,两边之差小于第三边可求得b的范围,进而利用余弦定理表示出cosC的表达式,根据b的范围求得cosC的范围,进而求得C的范围.
解答:因为c=AB=1,a=BC=2,b=AC
根据两边之和大于第三边,两边之差小于第三边可知
1<b<3,根据余弦定理
cosC=
 (a2+b2-c2)
(a2+b2-c2)=
 (4+b2-1)
(4+b2-1)=
 (3+b2)
(3+b2)=
 +
+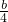
=
 (
( -
- )2+
)2+ ≥
≥
所以0<C≤30°
故选A
点评:本题主要考查了解三角形问题.考查了学生分析问题的基本的推理能力.

练习册系列答案
相关题目
已知在△ABC中,若
•
=
•
,则△ABC的形状是( )
| AB |
| AC |
| BA |
| BC |
| A、直角三角形 |
| B、正三角形 |
| C、等腰三角形 |
| D、等腰直角三角形 |
 (1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知
(1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知