题目内容
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 经过抛物线
经过抛物线![]() 与坐标轴的三个交点.
与坐标轴的三个交点.
(1)求圆![]() 的方程;
的方程;
(2)经过点![]() 的直线
的直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,若圆
两点,若圆![]() 在
在![]() ,
,![]() 两点处的切线互相垂直,求直线
两点处的切线互相垂直,求直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() 和
和![]() .
.
【解析】
(1)方法一、求得抛物线与坐标轴的三个交点,设出圆的一般式方程,代入三点坐标,解方程组可得D,E,F,即可得到所求圆方程;方法二、由抛物线方程与圆的一般式方程,可令y=0,可得D,F,再由抛物线与y轴的交点,可得E,即可得到所求圆方程;
(2)求圆C的圆心和半径,圆C在A,B两点处的切线互相垂直,可得∠ACB![]() ,求得C到直线l的距离,讨论直线l的斜率是否存在,由点到直线的距离公式,计算可得所求直线方程.
,求得C到直线l的距离,讨论直线l的斜率是否存在,由点到直线的距离公式,计算可得所求直线方程.
(1)方法一:抛物线![]() 与坐标轴的三个交点坐标为
与坐标轴的三个交点坐标为![]() ,
,![]() ,
,![]() .
.
设圆![]() 的方程为
的方程为![]() ,
,
则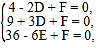 , 解得
, 解得 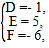
所以圆![]() 的方程为
的方程为![]() .
.
方法二:设圆![]() 的方程为
的方程为![]() .
.
令![]() ,得
,得![]() .
.
因为圆![]() 经过抛物线
经过抛物线![]() 与
与![]() 轴的交点,
轴的交点,
所以![]() 与方程
与方程![]() 同解,
同解,
所以![]() ,
,![]() .
.
因此圆![]() .
.
因为抛物线![]() 与
与![]() 轴的交点坐标为
轴的交点坐标为![]() ,
,
又所以点![]() 也在圆
也在圆![]() 上,所以
上,所以![]() ,解得
,解得![]() .
.
所以圆![]() 的方程为
的方程为![]() .
.
(2)由(1)可得,圆:![]() ,
,
故圆心![]() ,半径
,半径![]() .
.
因为圆![]() 在
在![]() ,
,![]() 两点处的切线互相垂直,所以
两点处的切线互相垂直,所以![]() .
.
所以![]() 到直线
到直线![]() 的距离
的距离![]() .
.
① 当直线![]() 的斜率不存在时,
的斜率不存在时,![]() ,符合题意;
,符合题意;
② 当直线![]() 的斜率存在时,设
的斜率存在时,设![]() ,即
,即![]() ,
,
所以![]() ,解得
,解得![]() ,
,
所以直线![]() ,即
,即![]() .
.
综上,所求直线![]() 的方程为
的方程为![]() 和
和![]() .
.
方法三:①当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
![]() ,
,![]() ,将直线
,将直线![]() 的方程代入圆
的方程代入圆![]() 的方程得:
的方程得:
![]() ,
,
即![]()
![]() ,
,![]() .
.
因为圆![]() 在点
在点![]() ,
,![]() 两点处的切线互相垂直,所以
两点处的切线互相垂直,所以![]() ,
,
所以![]() ,即
,即![]() ,
,
所以![]() ,
,
即![]() ,
,
即![]() ,
,
![]() ,
,
即![]() ,解得
,解得![]() ,所以直线
,所以直线![]() :
:![]() ,
,
即![]() .
.
②当直线![]() 的斜率不存在时,
的斜率不存在时,![]() :
:![]() ,符合题意;
,符合题意;
综上,所求直线![]() 的方程为
的方程为![]() 和
和![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某企业常年生产一种出口产品,根据预测可知,进入21世纪以来,该产品的产量平稳增长.记2009年为第1年,且前4年中,第x年与年产量f(x) 万件之间的关系如下表所示:
x | 1 | 2 | 3 | 4 |
f(x) | 4.00 | 5.58 | 7.00 | 8.44 |
若f(x)近似符合以下三种函数模型之一:f(x)=ax+b,f(x)=2x+a,f(x)=log![]() x+a.
x+a.
(1)找出你认为最适合的函数模型,并说明理由,然后选取其中你认为最适合的数据求出相应的解析式;
(2)因遭受某国对该产品进行反倾销的影响,2015年的年产量比预计减少30%,试根据所建立的函数模型,确定2015年的年产量.