题目内容
12．在平行四边形ABCD中，若$\overrightarrow{AC}$=$\overrightarrow{a}$，$\overrightarrow{BD}$=$\overrightarrow{b}$，则$\overrightarrow{AB}$=（ ）| A． | $\frac{1}{2}$（$\overrightarrow{a}$+$\overrightarrow{b}$） | B． | $\frac{1}{2}$（$\overrightarrow{a}$-$\overrightarrow{b}$） | C． | $\frac{1}{2}$（$\overrightarrow{b}$-$\overrightarrow{a}$） | D． | $\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ |
分析 根据题意，设AC与BD相交与点O，分析可得$\overrightarrow{AO}$=$\frac{1}{2}$$\overrightarrow{AC}$，$\overrightarrow{BO}$=$\frac{1}{2}$$\overrightarrow{BD}$，由向量的三角形法则可得$\overrightarrow{AB}$=$\overrightarrow{AO}$+$\overrightarrow{OB}$=$\overrightarrow{AO}$-$\overrightarrow{BO}$，代入即可得答案．
解答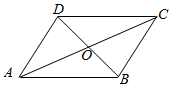 
解：根据题意，设AC与BD相交于点O，
则$\overrightarrow{AO}$=$\frac{1}{2}$$\overrightarrow{AC}$，$\overrightarrow{BO}$=$\frac{1}{2}$$\overrightarrow{BD}$，
则$\overrightarrow{AB}$=$\overrightarrow{AO}$+$\overrightarrow{OB}$=$\overrightarrow{AO}$-$\overrightarrow{BO}$=$\frac{1}{2}$（$\overrightarrow{AC}$-$\overrightarrow{BD}$）=$\frac{1}{2}$（$\overrightarrow{a}$-$\overrightarrow{b}$）；
故选：B．
点评 本题考查向量加法的几何意义，注意作出平行四边形，利用向量的加减运算的几何意义进行分析．
练习册系列答案
相关题目
2．函数f（x）=log2（x+3）（x-5）的定义域是A，函数g（x）=x3+m在x∈[1，2]上的值域为B，又已知B⊆A，则实数m的取值范围是（ ）
| A． | （-∞，-11）∪（4，+∞） | B． | （-11，4） | C． | （-4，-3） | D． | （-∞，-4]∪[-3，+∞） |
20．在等差数列{an}中，若a1、a10是方程2x2+5x+1=0的两个根，则公差d（d＞0）为（ ）
| A． | $\frac{\sqrt{17}}{18}$ | B． | $\frac{\sqrt{15}}{11}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{1}{2}$ |
7．已知函数f（x）=xsinx，则f（$\frac{π}{11}$），f（-1），f（-$\frac{π}{3}$）的大小关系为（ ）
| A． | f（-$\frac{π}{3}$）＞f（-1）＞f（$\frac{π}{11}$） | B． | f（-1）＞f（-$\frac{π}{3}$）＞f（$\frac{π}{11}$） | C． | f（-$\frac{π}{11}$）＞f（-1）＞f（$\frac{π}{3}$） | D． | f（$\frac{π}{3}$）＞f（$\frac{π}{11}$）＞f（-1） |
如图，在三棱锥A-BCD中，AB⊥BD，AD⊥CD，M，N分别为AC，BC的中点，且△BMC为正三角形．求证：
4．第五届北京农业嘉年华于2017年3月11日至5月7日在昌平区兴寿镇草莓博览园中举办，设置“三馆两园一带一谷一线”八大功能板块．现安排六名志愿者去其中的“三馆两园”参加志愿者服务工作，若每个“馆”与“园”都至少安排一人，则不同的安排方法种数为（ ）
| A． | C${\;}_{6}^{2}$A${\;}_{5}^{5}$ | B． | 5C${\;}_{6}^{1}$A${\;}_{5}^{5}$ | C． | 5A${\;}_{5}^{5}$ | D． | C${\;}_{6}^{1}$A${\;}_{5}^{5}$ |
1．
已知直三棱柱ABC-A1B1C1的各条棱长均为4，M是AB1的中点，连接BM、CM，则三棱锥B-ACM的体积等于（ ）
已知直三棱柱ABC-A1B1C1的各条棱长均为4，M是AB1的中点，连接BM、CM，则三棱锥B-ACM的体积等于（ ）| A． | $\frac{8}{3}$ | B． | $\frac{{8\sqrt{3}}}{3}$ | C． | $8\sqrt{3}$ | D． | $4\sqrt{3}$ |