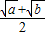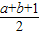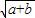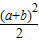题目内容
设a,b,x,y均为正数,且a,b为常数,x,y为变量,若x+y=1,则
+
的最大值为( )
| ax |
| by |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
分析:设x=sin2ω,y=cos2ω,利用辅角公式对
+
化简整理,根据正弦函数的性质求得答案.
| ax |
| by |
解答:解:设x=sin2ω,y=cos2ω,ω∈(0,
)
则
+
=
sinω+
cosω=
sin(ω+α)其中tanα=
当取ω=
-α时,有最大值
故选C
| π |
| 2 |
则
| ax |
| by |
| a |
| b |
| a+b |
| ||
|
当取ω=
| π |
| 2 |
| a+b |
故选C
点评:本题主要考查了利用三角函数求最值的问题.考查了学生对三角函数知识的综合运用.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
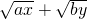 的最大值为
的最大值为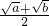

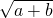
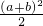
 的最大值为( )
的最大值为( )