题目内容
已知点P（a，b）（ab≠0）是圆O：x2+y2=r2内一点，直线l的方程为ax+by+r2=0，那么直线l与圆O的位置关系是
- A.相离
- B.相切
- C.相交
- D.不确定
A
分析：由题意可得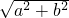
＜半径r，求出圆心（0，0）到直线的距离大于半径，可得直线和圆相离，从而得到答案．
解答：∵点P（a，b）（ab≠0）是圆O：x2+y2=r2内一点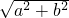，∴＜半径r．
圆心（0，0）到直线ax+by+r2=0的距离等于
＞
=r，
故直线和圆相离，
故选A．
点评：本题主要考查直线和圆的位置关系，点到直线的距离公式的应用，属于中档题．
分析：由题意可得
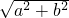＜半径r，求出圆心（0，0）到直线的距离大于半径，可得直线和圆相离，从而得到答案．解答：∵点P（a，b）（ab≠0）是圆O：x2+y2=r2内一点，∴
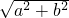＜半径r．圆心（0，0）到直线ax+by+r2=0的距离等于
＞=r，故直线和圆相离，
故选A．
点评：本题主要考查直线和圆的位置关系，点到直线的距离公式的应用，属于中档题．
练习册系列答案
相关题目
已知点P（a，b）（ab≠0）是圆O：x2+y2=r2内一点，直线m是以P为中点的弦所在的直线，若直线n的方程为ax+by=r2，则（ ）
| A、m∥n且n与圆O相离 | B、m∥n且n与圆O相交 | C、m与n重合且n与圆O相离 | D、m⊥n且n与圆O相离 |
已知点P，A，B，C，D是球O表面上的点，PA⊥平面ABCD，四边形ABCD的边长为
的正方形．若PA=
，则球O的表面积为（ ）
| 3 |
| 6 |
| A、9π | B、12π |
| C、18π | D、6π |