题目内容
求下列函数的定义域：（1）y=
+lgcosx;
(2)y=
+
.
解析：（1）要使函数y=+lgcosx有意义，必须且只需
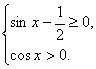
解得+2kπ≤x＜
+2kπ(k∈Z).
因此函数y=
+lgcosx的定义域是{x｜
+2kπ≤x＜
+2kπ,k∈Z,x∈R
.
（2）要使函数y=
+
有意义，必须且只需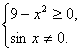
解得-3≤x＜0或0＜x≤3.
因此函数y=
+
的定义域是［-3,0
∪(0,3
.
练习册系列答案
相关题目
题目内容
求下列函数的定义域：（1）y=+lgcosx;
(2)y=+.
解析：（1）要使函数y=+lgcosx有意义，必须且只需
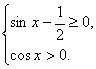
解得+2kπ≤x＜+2kπ(k∈Z).
因此函数y=+lgcosx的定义域是{x｜+2kπ≤x＜+2kπ,k∈Z,x∈R.
（2）要使函数y=+有意义，必须且只需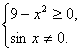
解得-3≤x＜0或0＜x≤3.
因此函数y=+的定义域是［-3,0∪(0,3.