题目内容
如图. 直三棱柱ABC —A1B1C1 中,A1B1= A1C1,点D、E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1的中点。
求证:(1)平面ADE⊥平面BCC1B1
(2)直线A1F∥平面ADE。
 |
(1) ABC—A1B1C1是直三棱柱,
ABC—A1B1C1是直三棱柱, CC1⊥面ABC,
CC1⊥面ABC,
又AD 平面ABC,
平面ABC, CC1⊥AD
CC1⊥AD
又 AD⊥DE,CC1,DE
AD⊥DE,CC1,DE 平面B CC1B1,CC1∩DE=E
平面B CC1B1,CC1∩DE=E
 AD⊥面B CC1 B1 又AD
AD⊥面B CC1 B1 又AD 面ADE
面ADE
 平面ADE⊥平面BCC1B1 …6分
平面ADE⊥平面BCC1B1 …6分
(2) A1B1= A1C1,F为B1C1的中点,
A1B1= A1C1,F为B1C1的中点, AF⊥B1C1
AF⊥B1C1
 CC1⊥面A1B1C1且A,F
CC1⊥面A1B1C1且A,F 平面A1B1C1
平面A1B1C1
 CC1⊥A、F
CC1⊥A、F
又CC1,A,F 平面BCC1B1,CC1∩B1C1= C1
平面BCC1B1,CC1∩B1C1= C1
 A1F⊥平面BCC1B1 由(1)知AD ⊥平面BCC1B1
A1F⊥平面BCC1B1 由(1)知AD ⊥平面BCC1B1
 A1F∥AD,又AD
A1F∥AD,又AD 平面ADE,A1F
平面ADE,A1F 平面ADE
平面ADE
 A1F∥平面ADE …12分
A1F∥平面ADE …12分

练习册系列答案
相关题目
 与曲线
与曲线 所围成的封闭图形的面积为 ;
所围成的封闭图形的面积为 ; 满足
满足 则
则 ( )
( ) 的圆心到直线
的圆心到直线 的距离为 。
的距离为 。 B、
B、 C、
C、 D、
D、
 时,
时, ,则函数
,则函数 的零点的集合为
的零点的集合为 B、
B、 C、
C、
 D、
D、
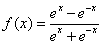 ,若
,若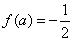 ,则
,则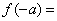 .
.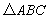 的周长为
的周长为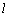 ,面积为
,面积为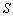 ,则
,则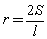 .将此结论类比到空间,已知四面体
.将此结论类比到空间,已知四面体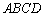 的表面积为
的表面积为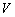 ,则四面体
,则四面体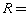 .
.