题目内容
(1)若a≥1,用分析法证明
+
<2
;
(2)已知a,b都是正实数,且ab=2,求证:(2a+1)(b+1)≥9.
| a+1 |
| a-1 |
| a |
(2)已知a,b都是正实数,且ab=2,求证:(2a+1)(b+1)≥9.
证明:(1)因a≥1,所以,要证
+
<2
,
只需证明a+1+2
+a-1<4a,即证
<a,
只需证明a2-1<a2,即-1<0,
此不等式显然成立,于是
+
<2
.
(2)因a,b都是正实数,所以,2a+b≥2
=4,当且仅当b=2a,即a=1,b=2时等号成立,
∴(2a+1)(b+1)=2ab+(2a+b)+1≥4+4+1=9.
| a+1 |
| a-1 |
| a |
只需证明a+1+2
| a2-1 |
| a2-1 |
只需证明a2-1<a2,即-1<0,
此不等式显然成立,于是
| a+1 |
| a-1 |
| a |
(2)因a,b都是正实数,所以,2a+b≥2
| 2ab |
∴(2a+1)(b+1)=2ab+(2a+b)+1≥4+4+1=9.

练习册系列答案
相关题目
 (a为实数).
(a为实数). 在
在 上是增函数;
上是增函数; 的图象与
的图象与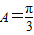 .
. ,求b+c的值;
,求b+c的值; 的值(注意,此问只能使用题干的条件,不能用(1)问的条件).
的值(注意,此问只能使用题干的条件,不能用(1)问的条件).