题目内容
在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD为平行四边形，PA=a，AB=2PA，∠ABC=60°，则D到平面PBC的距离为 ．
考点：点、线、面间的距离计算,棱锥的结构特征
专题：空间位置关系与距离
分析：以A为原点，取BC中点E以AE为x轴，以AD为y轴，以AP为z轴，建立空间直角坐标系，利用向量法能求出D到平面PBC的距离．
解答：
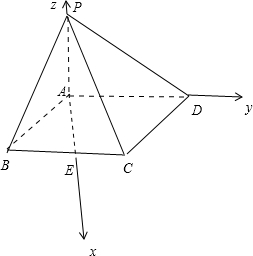解：如图，∵在四棱锥P-ABCD中，PA⊥平面ABCD，
底面ABCD为平行四边形，PA=a，AB=2PA，∠ABC=60°，
∴以A为原点，取BC中点E以AE为x轴，以AD为y轴，
以AP为z轴，建立空间直角坐标系，
D（0，2a，0），B（
a，-a，0），C（
a，a，0），P（0，0，a），
=(
a，-a，-a)，
=(
a，a，-a)，
设平面PBC的法向量
=(x，y，z)，
则
，
取x=
，得
=（
，0，3），
=（0，2a，-a），
∴D到平面PBC的距离：
d=
=
=
a．
故答案为：
a．
解：如图，∵在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD为平行四边形，PA=a，AB=2PA，∠ABC=60°，
∴以A为原点，取BC中点E以AE为x轴，以AD为y轴，
以AP为z轴，建立空间直角坐标系，
D（0，2a，0），B（
| 3 |
| 3 |
| PB |
| 3 |
| PC |
| 3 |
设平面PBC的法向量
| n |
则
|
取x=
| 3 |
| n |
| 3 |
| PD |
∴D到平面PBC的距离：
d=
|
| ||||
|
|
| |-3a| | ||
|
| ||
| 2 |
故答案为：
| ||
| 2 |
点评：本题考查点到平面的距离的求法，解题时要认真审题，注意向量法的合理运用．
练习册系列答案
相关题目
某多面体的三视图如图所示，按照给出的尺寸（单位：cm），则此几何体的体积为