题目内容
(本小题满分l 3分)在数列{an}中,a1=2,an+l=an+cn (n∈N*,常数c≠0),且a1,a2,a3成等比数列.
(I)求c的值;
(Ⅱ)求数列{an}的通项公式.
(I)求c的值;
(Ⅱ)求数列{an}的通项公式.
解:(Ⅰ)由题知, ,
,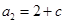 ,
,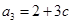 ,········ 2分
,········ 2分
因为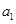 ,
,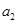 ,
, 成等比数列,所以
成等比数列,所以 ,·········· 4分
,·········· 4分
解得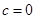 或
或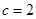 ,又
,又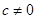 ,故
,故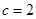 .·················· 6分
.·················· 6分
(Ⅱ)当 时,由
时,由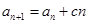 得
得
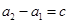 ,
,
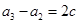 ,
,
…
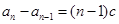 ,
,
以上各式相加,得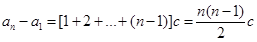 , ······· 9分
, ······· 9分
又 ,
,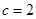 ,故
,故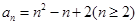 ,··············· 11分
,··············· 11分
当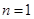 时上式也成立,························· 12分
时上式也成立,························· 12分
所以数列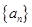 的通项公式为
的通项公式为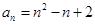 .(
.(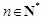 ).·········· 13分
).·········· 13分
 ,
,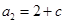 ,
,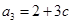 ,········ 2分
,········ 2分因为
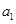 ,
,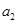 ,
, 成等比数列,所以
成等比数列,所以 ,·········· 4分
,·········· 4分解得
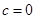 或
或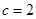 ,又
,又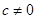 ,故
,故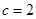 .·················· 6分
.·················· 6分(Ⅱ)当
 时,由
时,由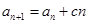 得
得
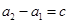 ,
,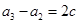 ,
,…
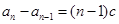 ,
,以上各式相加,得
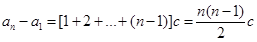 , ······· 9分
, ······· 9分又
 ,
,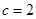 ,故
,故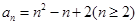 ,··············· 11分
,··············· 11分当
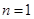 时上式也成立,························· 12分
时上式也成立,························· 12分所以数列
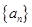 的通项公式为
的通项公式为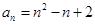 .(
.(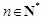 ).·········· 13分
).·········· 13分略

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
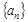 中,
中,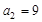 ,
,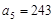 ,则
,则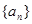 ,其前
,其前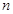 项和
项和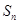 满足
满足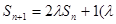 是大于0的常数),且
是大于0的常数),且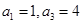
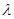 的值;
的值;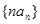 的前n项和为Tn,试比较
的前n项和为Tn,试比较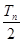 与Sn的大小.
与Sn的大小.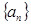 中,
中,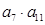 =6,
=6,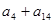 =5,则
=5,则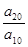 等于
等于 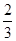
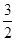
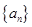 前
前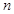 项和为
项和为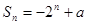 ,则复数
,则复数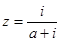 在复平面上对应的点位于 ( )
在复平面上对应的点位于 ( ) 
 ,则
,则 ( )
( )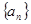 满足:
满足: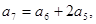 若存在两项
若存在两项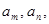 使得
使得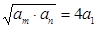 ,则
,则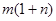 的最大值等于 .
的最大值等于 .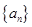 的前
的前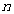 项和为
项和为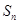 ,已知
,已知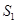 ,
,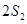 ,
,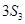 成等差数列,则
成等差数列,则
 个正数排成如右表所示的
个正数排成如右表所示的 行
行 ,其中第一行从左到右成等差数列,每一列从上到下成等比数列,且公比均相等。若已知
,其中第一行从左到右成等差数列,每一列从上到下成等比数列,且公比均相等。若已知 ,则
,则