题目内容
直线l：x+2y=4与圆C：x2+y2=9交于A、B两点，O是坐标原点，若直线OA、OB的倾斜面角分别为α，β，则sinα+sinβ=
- A.
- B.
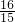
- C.
- D.
B
分析：由
可得 5y2-16y+7=0，可得 y1+y2 的值．再由任意角的三角函数的定义可得 sinα=
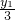，sinβ=
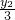，由此求得sinα+sinβ的值．
解答：由可得 5y2-16y+7=0，
∴y1+y2=，其中，y1 和y2 分别是A、B两点的纵坐标．
再由题意可得，OA=OB=3．再由任意角的三角函数的定义可得 sinα=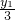，sinβ=，
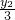故sinα+sinβ=+=，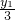
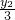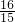故选B．
点评：本题主要考查直线和圆的位置关系，一元二次方程根与系数的关系，任意角的三角函数的定义，属于中档题．
分析：由
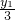可得 5y2-16y+7=0，可得 y1+y2 的值．再由任意角的三角函数的定义可得 sinα=，sinβ=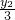，由此求得sinα+sinβ的值．解答：由
可得 5y2-16y+7=0，∴y1+y2=
，其中，y1 和y2 分别是A、B两点的纵坐标．再由题意可得，OA=OB=3．再由任意角的三角函数的定义可得 sinα=
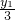，sinβ=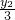，故sinα+sinβ=
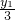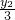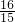+=，故选B．
点评：本题主要考查直线和圆的位置关系，一元二次方程根与系数的关系，任意角的三角函数的定义，属于中档题．
练习册系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
相关题目