题目内容
20.已知函数f(x)=(m-2)x2+(m-1)x+m3+3m+2为偶函数,则m=( )| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
分析 令f(-x)=f(x),根据多项式相等得出对应项系数相等,列出方程解出m.
解答 解:∵f(x)是偶函数,∴f(-x)=f(x),即(m-2)x2+(1-m)x+m3+3m+2=(m-2)x2+(m-1)x+m3+3m+2.
∴1-m=m-1,解得m=1.
故选:C.
点评 本题考查了函数奇偶性的性质,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.已知定义在R上的偶函数f(x),对任意x∈R满足f(x+1)=f(-x+1),当6≤x≤7时,f(x)=1g(x-5);则方程f(x)-1gx=-1+1g5的实数根个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
15.已知log${\;}_{\frac{1}{2}}$b<-log2a<-2log4c,则( )
| A. | b>a>c | B. | c>b>a | C. | c>a>b | D. | a>b>c |
5.△ABC的内角A,B,C的对边分别为a,b,c,若sinAsinC=$\frac{1}{4}$,b=$\sqrt{6}$,B=120°,则△ABC的面积等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
5.袋子中装有大小相同的6个小球,分别有2个红球、4个白球,现从中随机摸出3个小球,则至少有2个白球的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{7}{10}$ |
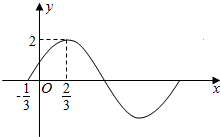 己知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)部分图象如图所示.
己知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)部分图象如图所示.