题目内容
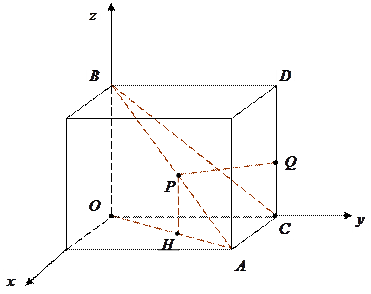
如图,以正方体的三条棱所在直线为坐标轴,建立空间直角坐标系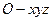 .点
.点 在正方体的对角线
在正方体的对角线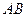 上,点
上,点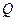 在正方体的棱
在正方体的棱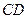 上.
上.
(1) 当点 为对角线
为对角线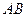 的中点,点
的中点,点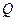 在棱
在棱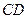 上运动时,探究
上运动时,探究 的最小值;
的最小值;
(2) 当点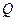 为棱
为棱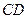 的中点,点
的中点,点 在对角线
在对角线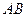 上运动时,探究
上运动时,探究 的最小值;
的最小值;
(3) 当点 在对角线
在对角线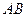 上运动,点
上运动,点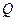 在棱
在棱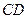 上运动时,探究
上运动时,探究 的最小值.
的最小值.
由以上问题,你得到了什么结论?你能证明你的结论吗?

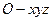 .点
.点 在正方体的对角线
在正方体的对角线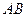 上,点
上,点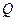 在正方体的棱
在正方体的棱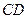 上.
上.(1) 当点
 为对角线
为对角线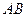 的中点,点
的中点,点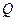 在棱
在棱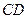 上运动时,探究
上运动时,探究 的最小值;
的最小值;(2) 当点
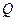 为棱
为棱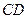 的中点,点
的中点,点 在对角线
在对角线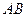 上运动时,探究
上运动时,探究 的最小值;
的最小值;(3) 当点
 在对角线
在对角线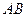 上运动,点
上运动,点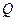 在棱
在棱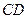 上运动时,探究
上运动时,探究 的最小值.
的最小值.由以上问题,你得到了什么结论?你能证明你的结论吗?

(1) 有最小值
有最小值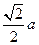 (2)
(2) 取得最小值
取得最小值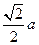 (3)最小值是
(3)最小值是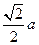
 有最小值
有最小值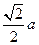 (2)
(2) 取得最小值
取得最小值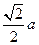 (3)最小值是
(3)最小值是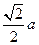
设正方体的棱长为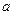 .
.
(1) 当点 为对角线
为对角线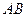 的中点时,点
的中点时,点 的坐标是
的坐标是 .
.
因为点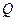 在线段
在线段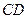 上,设
上,设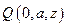 .
.
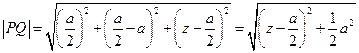 .
.
当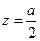 时,
时, 的最小值为
的最小值为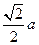 ,即点
,即点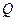 在棱
在棱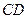 的中点时,
的中点时, 有最小值
有最小值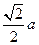 .
.
(2) 因为 在对角线
在对角线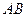 上运动.
上运动.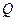 是定点,所以当
是定点,所以当
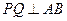 时,
时, 最短.因为当点
最短.因为当点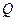 为棱
为棱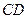 的中点时,
的中点时, ,
,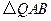 是等腰三角形,所以,当点
是等腰三角形,所以,当点 是
是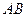 的中点时,
的中点时, 取得最小值
取得最小值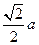 .
.
(3) 当点 在对角线
在对角线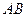 上运动,点
上运动,点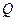 在棱
在棱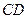 上运动
上运动
时, 的最小值仍然是
的最小值仍然是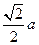 .
.
证明:如下图,设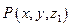 ,由正方体的对称性,显然有
,由正方体的对称性,显然有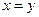 .
.
设 在平面
在平面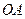 上的射影是
上的射影是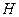 .在
.在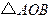 中,
中,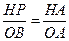 ,所以
,所以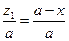 ,即有
,即有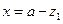 .
.
所以,点 的坐标是
的坐标是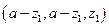 .
.
由已知,可设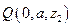 ,则
,则
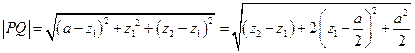 .
.
当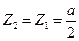 时,
时, 取得最小值,最小值是
取得最小值,最小值是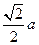 .
.
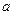 .
.(1) 当点
 为对角线
为对角线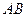 的中点时,点
的中点时,点 的坐标是
的坐标是 .
.因为点
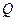 在线段
在线段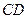 上,设
上,设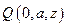 .
.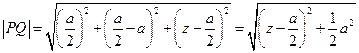 .
.当
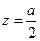 时,
时, 的最小值为
的最小值为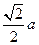 ,即点
,即点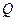 在棱
在棱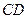 的中点时,
的中点时, 有最小值
有最小值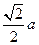 .
.(2) 因为
 在对角线
在对角线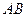 上运动.
上运动.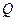 是定点,所以当
是定点,所以当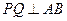 时,
时, 最短.因为当点
最短.因为当点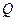 为棱
为棱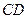 的中点时,
的中点时, ,
,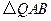 是等腰三角形,所以,当点
是等腰三角形,所以,当点 是
是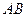 的中点时,
的中点时, 取得最小值
取得最小值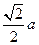 .
.(3) 当点
 在对角线
在对角线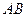 上运动,点
上运动,点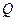 在棱
在棱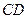 上运动
上运动时,
 的最小值仍然是
的最小值仍然是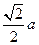 .
.证明:如下图,设
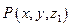 ,由正方体的对称性,显然有
,由正方体的对称性,显然有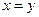 .
.设
 在平面
在平面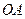 上的射影是
上的射影是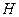 .在
.在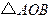 中,
中,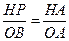 ,所以
,所以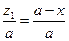 ,即有
,即有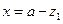 .
.所以,点
 的坐标是
的坐标是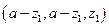 .
.由已知,可设
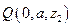 ,则
,则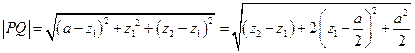 .
.当
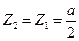 时,
时, 取得最小值,最小值是
取得最小值,最小值是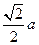 .
.

练习册系列答案
相关题目
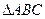 内接于以O为圆心,1为半径的圆,且
内接于以O为圆心,1为半径的圆,且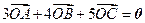 .
.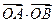 ,
,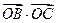 ,
,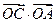 ;
; 若
若 ,则m=( )
,则m=( )

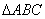 中,O为中线AM上一个动点,若AM=2,则
中,O为中线AM上一个动点,若AM=2,则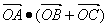 的最小值是_____.
的最小值是_____. 若
若 ,则
,则 的值为( )
的值为( )



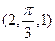 ,则点M的直角坐标是 。
,则点M的直角坐标是 。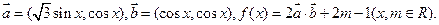
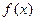 关于x的表达式,并求
关于x的表达式,并求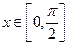 时,
时,