题目内容
已知平行六面体ABCD-A1B1C1D1中,点E是上底面A1B1C1D1(包括边界)内的任一点,若
=x
+y
+z
,则x,y,z满足的关系式为:______.
| AE |
| AA1 |
| AB |
| AD |
在平行六面体ABCD-A1B1C1D1中,因为点E是上底面A1B1C1D1(包括边界)内的任一点,
所以根据向量的加法得
=
+
,
在底面A1B1C1D1内,根据平面向量的基本定理可得
=y
+z
.(0≤y≤1,0≤z≤1),
所以
=
+y
+z
,
所以x=1,0≤y≤1,0≤z≤1.
故答案为:x=1,0≤y≤1,0≤z≤1..
所以根据向量的加法得
| AE |
| AA1 |
| A1E |
在底面A1B1C1D1内,根据平面向量的基本定理可得
| A1E |
| A1B1 |
| A1D1 |
所以
| AE |
| AA1 |
| A1B1 |
| A1D1 |
所以x=1,0≤y≤1,0≤z≤1.
故答案为:x=1,0≤y≤1,0≤z≤1..

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
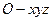 .点
.点 在正方体的对角线
在正方体的对角线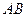 上,点
上,点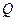 在正方体的棱
在正方体的棱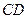 上.
上. 的最小值;
的最小值;
 =
= ,
, =
= ,且
,且 的取值范围
的取值范围
 .
. 证明:
证明: ;
; ,求
,求 .
. =2a+pb,
=2a+pb, =a+b,
=a+b, =a-2b.若A、B、D三点共线,则实数p=________.
=a-2b.若A、B、D三点共线,则实数p=________. 中,
中, 是
是 边中点,角
边中点,角 ,
, ,
, 的对边分别是
的对边分别是 ,
, ,
, ,若
,若 ,则
,则 中,点
中,点 是
是 上的点,
上的点, ,则( ).
,则( ).



 、
、 、
、 ,点
,点 在平面
在平面 内,则
内,则 的值为( )
的值为( )