题目内容
已知数列{an}有a1=a,a2=p(常数 p>0),对任意的正整数n,Sn=a1+a2+…+an,并有Sn满足![]() .
.
(1)求a的值;
(2)试确定数列{an}是否是等差数列,若是,求出其通项公式,若不是,说明理由;
(3)(理科生答文科生不答)对于数列{bn},假如存在一个常数![]() 使得对任意的正整数n都有bn<b,且
使得对任意的正整数n都有bn<b,且![]() ,则称b为数列{bn}的“上渐近值”,令
,则称b为数列{bn}的“上渐近值”,令![]() ,求数列{p1+p2+…+pn-2n}的“上渐近值”.
,求数列{p1+p2+…+pn-2n}的“上渐近值”.
答案:
解析:
解析:
|
所以数列 (文)解:(1)在 (2)由第(1)步知 所以: 因此当 故 并且 所以 |

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目

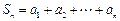 ,且
,且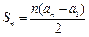 .
.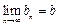 ,则称b为数列{bn}的“上渐近值”,令
,则称b为数列{bn}的“上渐近值”,令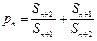 ,求数列
,求数列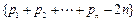 的“上渐近值”.
的“上渐近值”.