题目内容

中心在坐标原点，一个焦点为（5，0），且以直线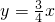 $数学公式$ 为渐近线的双曲线方程为 ________．

$\text{[math]}$
分析：设双曲线方程为 $\text{[math]}$ + $\text{[math]}$ =1，由5= $\text{[math]}$ ①，和 $\text{[math]}$ = $\text{[math]}$ ②，解方程组求得 a²，b² 的值．
解答：设双曲线方程为 $\text{[math]}$ + $\text{[math]}$ =1，由题意得 c=5= $\text{[math]}$ ①， $\text{[math]}$ = $\text{[math]}$ ②，
由 ①②得 a²=16，b²=9，故所求的双曲线方程为 $\text{[math]}$ - $\text{[math]}$ =1，
故答案为： $\text{[math]}$ - $\text{[math]}$ =1．
点评：本题考查利用待定系数法求双曲线的标准方程的方法，以及双曲线的简单性质得应用．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

已知双曲线的中心在坐标原点，一个焦点为F（10，0），两条渐近线的方程为y=±

x，则该双曲线的标准方程为

已知；椭圆C的对称中心在坐标原点，一个顶点为A（0，2），左焦点为F(-2

， 0)．
（Ⅰ）求椭圆C的方程；
（Ⅱ）是否存在过点B（0，-2）的直线l，使直线l与椭圆C相交于不同的两点M、N，并满足|AM|=|AN|，若存在，求直线l的方程；若不存在，说明理由．

中心在坐标原点，一个焦点为（5，0），且以直线y=±

x为渐近线的双曲线方程为

=1（a＞b＞0）的面积为s=abπ．现有一个椭圆，其中心在坐标原点，一个焦点坐标为（4，0），且长轴长与短轴长的差为2，则该椭圆的面积为（　　）

已知过点A（0，4）的直线l与以F为焦点的抛物线C：x²=py相切于点T（-4，y_o）；中心在坐标原点，一个焦点为F的椭圆与直线l有公共点．
（1）求直线l的方程和焦点F的坐标；
（2）求当椭圆的离心率最大时椭圆的方程；
（3）设点M（x₁，y_l）是抛物线C上任意一点，D（0，-2）为定点，是否存在垂直于y轴的直线l′被以MD为直径的圆截得的弦长为定值？请说明理由．