题目内容
已知二次函数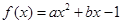 ,且不等式
,且不等式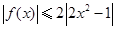 对任意的实数
对任意的实数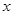 恒成立,数列
恒成立,数列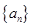 满足
满足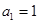 ,
,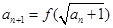
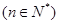 .
.
(1)求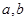 的值;
的值;
(2)求数列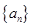 的通项公式;
的通项公式;
(3)求证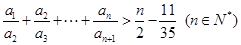 .
.
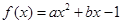 ,且不等式
,且不等式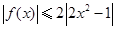 对任意的实数
对任意的实数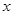 恒成立,数列
恒成立,数列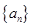 满足
满足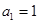 ,
,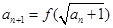
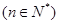 .
.(1)求
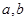 的值;
的值;(2)求数列
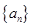 的通项公式;
的通项公式;(3)求证
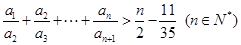 .
.(1) (2)
(2)
(3)




 综上有
综上有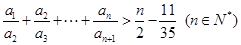
 (2)
(2)
(3)





 综上有
综上有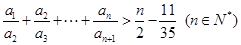
试题分析:⑴
 不等式
不等式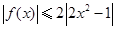 对任意的实数
对任意的实数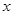 恒成立.
恒成立. 当
当 或
或 时,
时, ,解得:
,解得: ;
;⑵由⑴知
 ,
,
 ,
,

又
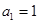 ,
, 数列
数列 是以
是以 为首项,2为公比的等比数列.
为首项,2为公比的等比数列.
 ,从而数列
,从而数列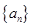 的通项公式
的通项公式 ;
;⑶由⑵知
 ,
,
 (
( )
)又






综上有
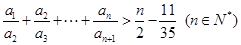 .
.点评:本题第二问是由数列递推公式
 通过构造新数列转化为等比数列求出
通过构造新数列转化为等比数列求出 通项,这是求通项的题目中经常考到的题型,第三问的证明主要利用的是放缩法,这种方法要求技巧性比较强,对学生是一个难点,不易掌握
通项,这是求通项的题目中经常考到的题型,第三问的证明主要利用的是放缩法,这种方法要求技巧性比较强,对学生是一个难点,不易掌握
练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 的首项
的首项 ,且
,且 ,则
,则 为( )
为( ) 是等差数列,其前
是等差数列,其前 项和为
项和为 ,已知
,已知
 ,证明:
,证明: 是等比数列,并求其前
是等比数列,并求其前 .
. ,求其前
,求其前
 中,若
中,若 ,则
,则 等于( )
等于( )  的前
的前 项和
项和 ,且满足
,且满足 .
. 的值,猜想
的值,猜想 是数列
是数列 的前
的前 .
.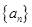 是等差数列,且满足:
是等差数列,且满足: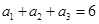 ,
,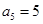 ;数列
;数列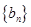 满足
满足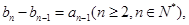
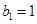 .
.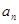 和
和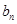 ;
;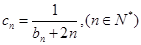 ,若
,若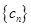 的前
的前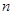 项和为
项和为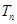 ,求证
,求证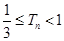 .
. 中,已知
中,已知 ,
, ,
, ,则
,则 是( )
是( ) ,数列
,数列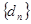 满足
满足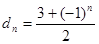 ,数列
,数列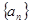 满足
满足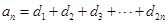 ;又知数列
;又知数列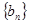 中,
中,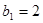 ,且对任意正整数
,且对任意正整数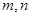 ,
,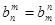 .
.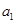 项,第
项,第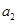 项,第
项,第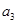 项,……,第
项,……,第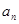 项,……删去后,剩余的项按从小到大的顺序排成新数列
项,……删去后,剩余的项按从小到大的顺序排成新数列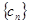 ,求数列
,求数列 项和.
项和.