题目内容
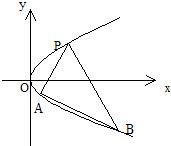 如图,过抛物线y2=2px(p>0)上一定点P(x0,y0)(y0>0),作两条直线分别交抛物线于A(x1,y1),B(x2,y2)
如图,过抛物线y2=2px(p>0)上一定点P(x0,y0)(y0>0),作两条直线分别交抛物线于A(x1,y1),B(x2,y2)(I)求该抛物线上纵坐标为
| p |
| 2 |
(II)当PA与PB的斜率存在且倾斜角互补时,求
| y1+y2 |
| y0 |
分析:(I)把y=
代入抛物线方程求得x,进而利用抛物线的方程推断出准线方程,最后根据抛物线的定义求得答案.
(II)设出直线PA,PB的斜率,把A,P点代入抛物线的方程相减后,表示出两直线的斜率,利用其倾斜角互补推断出
kPA=-kPB,求得三点纵坐标的关系式,同样把把A,B点代入抛物线的方程相减后,表示出AB的斜率,将y1+y2=-2y0代入求得结果为非零常数.
| p |
| 2 |
(II)设出直线PA,PB的斜率,把A,P点代入抛物线的方程相减后,表示出两直线的斜率,利用其倾斜角互补推断出
kPA=-kPB,求得三点纵坐标的关系式,同样把把A,B点代入抛物线的方程相减后,表示出AB的斜率,将y1+y2=-2y0代入求得结果为非零常数.
解答: 解:(I)当y=
解:(I)当y=
时,x=
又抛物线y2=2px的准线方程为x=-
由抛物线定义得,所求距离为
-(-
)=
(II)设直线PA的斜率为kPA,直线PB的斜率为kPB
由y12=2px1,y02=2px0
相减得(y1-y0)(y1+y0)=2p(x1-x0)
故kPA=
=
(x1≠x0)
同理可得kPB=
(x2≠x0)
由PA,PB倾斜角互补知kPA=-kPB
即
=-
所以y1+y2=-2y0
故
=-2
设直线AB的斜率为kAB
由y22=2px2,y12=2px1
相减得(y2-y1)(y2+y1)=2p(x2-x1)
所以kAB=
=
(x1≠x2)
将y1+y2=-2y0(y0>0)代入得kAB=
=-
,所以kAB是非零常数
 解:(I)当y=
解:(I)当y=| p |
| 2 |
| p |
| 8 |
又抛物线y2=2px的准线方程为x=-
| p |
| 2 |
由抛物线定义得,所求距离为
| p |
| 8 |
| p |
| 2 |
| 5p |
| 8 |
(II)设直线PA的斜率为kPA,直线PB的斜率为kPB
由y12=2px1,y02=2px0
相减得(y1-y0)(y1+y0)=2p(x1-x0)
故kPA=
| y1-y0 |
| x1-x0 |
| 2p |
| y1+y0 |
同理可得kPB=
| 2p |
| y2+y0 |
由PA,PB倾斜角互补知kPA=-kPB
即
| 2p |
| y1+y0 |
| 2p |
| y2+y0 |
所以y1+y2=-2y0
故
| y1+y2 |
| y0 |
设直线AB的斜率为kAB
由y22=2px2,y12=2px1
相减得(y2-y1)(y2+y1)=2p(x2-x1)
所以kAB=
| y2-y1 |
| x2-x1 |
| 2p |
| y1+y2 |
将y1+y2=-2y0(y0>0)代入得kAB=
| 2p |
| y1+y2 |
| p |
| y0 |
点评:本小题主要考查直线、抛物线等基本知识,考查运用解析几何的方法分析问题和解决问题的能力.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
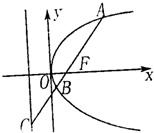 如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为
如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为 78、如图,过抛物线y2=4x的焦点F的直线交抛物线与圆(x-1)2+y2=1于A,B,C,D四点,则|AB|•|CD|=
78、如图,过抛物线y2=4x的焦点F的直线交抛物线与圆(x-1)2+y2=1于A,B,C,D四点,则|AB|•|CD|= 如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B(|AF|>|BF|),交其准线于点C,若|BC|=2|BF|,且|AF|=2,则此抛物线的方程为
如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B(|AF|>|BF|),交其准线于点C,若|BC|=2|BF|,且|AF|=2,则此抛物线的方程为 如图,过抛物线y2=2px(p>0)的焦点F且倾斜角为60°的直线l交抛物线于A、B两点,若|AF|=3,则此抛物线方程为( )
如图,过抛物线y2=2px(p>0)的焦点F且倾斜角为60°的直线l交抛物线于A、B两点,若|AF|=3,则此抛物线方程为( ) 如图,过抛物线y2=4x焦点的直线依次交抛物线与圆(x-1)2+y2=1于A,B,C,D,则
如图,过抛物线y2=4x焦点的直线依次交抛物线与圆(x-1)2+y2=1于A,B,C,D,则