题目内容
设椭圆的对称中心为坐标原点,其中一个顶点为A(0,2),右焦点F与点B(| 2 |
| 2 |
(1)求椭圆的方程;
(2)是否存在经过点(0,-3)的直线l,使直线l与椭圆相交于不同的两点M,N满足|
| AM |
| AN |
分析:(1)直接根据条件得到(c-
)2+2=4以及b=2;求出a2=12即可得到椭圆的方程;
(2)设直线l的方程为y=kx-3(k≠0),由|AM|=|AN|知点A在线段MN的垂直平分线上;联立直线方程和椭圆方程得到k的屈指范围以及点M,N的坐标和k的关系,结合点A在线段MN的垂直平分线对应的斜率相乘等于-1即可求出结论.
| 2 |
(2)设直线l的方程为y=kx-3(k≠0),由|AM|=|AN|知点A在线段MN的垂直平分线上;联立直线方程和椭圆方程得到k的屈指范围以及点M,N的坐标和k的关系,结合点A在线段MN的垂直平分线对应的斜率相乘等于-1即可求出结论.
解答:解:(1)依题意,设椭圆方程为
+
=1 ( a>b>0 ),
则其右焦点坐标为F(c , 0 ) ,c=
,由|FB|=2,
得
=2,即(c-
)2+2=4,故c=2
.
又∵b=2,∴a2=12,
从而可得椭圆方程为
+
=1.--(6分)
(2)由题意可设直线l的方程为y=kx-3(k≠0),由|AM|=|AN|知点A在线段MN的垂直平分线上,
由
消去y得x2+3(kx-3)2=12,即可得方程(1+3k2)x2-18kx+15=0…(*)
当方程(*)的△=(-18k)2-4(1+3k2)×15=144k2-60>0
即k2>
时方程(*)有两个不相等的实数根.
设M(x1,y1),N(x2,y2),线段MN的中点P(x0,y0),
则x1,x2是方程(*)的两个不等的实根,故有x1+x2=
.
从而有 x0=
=
,y0=kx0-3=
=
.
于是,可得线段MN的中点P的坐标为P (
,
)
又由于k≠0,因此直线AP的斜率为k1=
=
,
由AP⊥MN,得
×k=-1,即5+6k2=9,解得k2=
>
,
∴k=±
,
∴综上可知存在直线l:y=±
x-3满足题意.--------(13分)
| x2 |
| a2 |
| y2 |
| b2 |
则其右焦点坐标为F(c , 0 ) ,c=
| a2-b2 |
得
(c-
|
| 2 |
| 2 |
又∵b=2,∴a2=12,
从而可得椭圆方程为
| x2 |
| 12 |
| y2 |
| 4 |
(2)由题意可设直线l的方程为y=kx-3(k≠0),由|AM|=|AN|知点A在线段MN的垂直平分线上,
由
|
当方程(*)的△=(-18k)2-4(1+3k2)×15=144k2-60>0
即k2>
| 5 |
| 12 |
设M(x1,y1),N(x2,y2),线段MN的中点P(x0,y0),
则x1,x2是方程(*)的两个不等的实根,故有x1+x2=
| 18k |
| 1+3k2 |
从而有 x0=
| x1+x2 |
| 2 |
| 9k |
| 1+3k2 |
| 9k2-3 (1+3k2) |
| 1+3k2 |
| -3 |
| 1+3k2 |
于是,可得线段MN的中点P的坐标为P (
| 9k |
| 1+3k2 |
| -3 |
| 1+3k2 |
又由于k≠0,因此直线AP的斜率为k1=
| ||
|
| -5-6k2 |
| 9k |
由AP⊥MN,得
| -5-6k2 |
| 9k |
| 2 |
| 3 |
| 5 |
| 12 |
∴k=±
| ||
| 3 |
∴综上可知存在直线l:y=±
| ||
| 3 |
点评:本题考查了椭圆的标准方程、直线与圆锥曲线的位置关系,是一道综合性的试题,考查了学生综合运用知识解决问题的能力.

练习册系列答案
相关题目
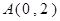 ,右焦点
,右焦点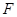 与点
与点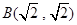 的距离为
的距离为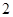 .
.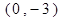 的直线
的直线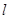 ,使直线
,使直线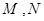 满足
满足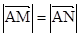 ?若存在,求出直线
?若存在,求出直线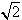 ,
,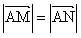 ?若存在,求直线l的倾斜角α;若不存在,请说明理由。
?若存在,求直线l的倾斜角α;若不存在,请说明理由。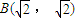 的距离为2.
的距离为2.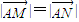 ?若存在,求出直线l的方程;若不存在,请说明理由.
?若存在,求出直线l的方程;若不存在,请说明理由.