题目内容
13.已知函数f(x)=sin(ωx+φ),ω>0,|φ|<$\frac{π}{2}$的部分图象如图所示,则f($\frac{π}{2}$)为( )
| A. | 1 | B. | -1 | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
分析 由周期求出ω,由特殊点的坐标求出φ的值,可得函数的f(x)的解析式,从而求得f($\frac{π}{2}$)的值.
解答 解:根据函数f(x)=sin(ωx+φ),ω>0,|φ|<$\frac{π}{2}$的部分图象,
可得$\frac{T}{2}=\frac{3π}{4}-\frac{5π}{12}=\frac{π}{ω}$,∴ω=3,
将($\frac{7π}{12}$,-1)代入,可得sin($\frac{7π}{4}$+φ)=-1,|φ|<$\frac{π}{2}$,∴φ=-$\frac{π}{4}$,
∴f(x)=sin(3x-$\frac{π}{4}$),
∴f($\frac{π}{2}$)=sin$\frac{5π}{4}$=-$\frac{\sqrt{2}}{2}$,
故选D.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由周期求出ω,由特殊点的坐标求出φ的值,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.函数y=x2+bx+c在[0,+∞)上是单调函数的充分条件是( )
| A. | b>1 | B. | b<-1 | C. | b<0 | D. | b>-1 |
1.若a1、b1、c1、a2、b2、c2∈R,且都不为零,则“$\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}$”是“关于x的不等式a1x2+b1x+c1>0与a2x2+b2x+c2>0的解集相同”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
3.某个体服装店经营某种服装,一周内获纯利y(元)与该周每天销售这种服装的件数x之间的一组数据如表:
已知:$\sum_{i=1}^{7}$xi2=280,$\sum_{i=1}^{7}$yi2=45309,$\sum_{i=1}^{7}$xiyi=3487
(1)求$\overline{x}$,$\overline{y}$;
(2)纯利润y与每天销售件数x之间线性相关,求出线性回归方程.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
| x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
(1)求$\overline{x}$,$\overline{y}$;
(2)纯利润y与每天销售件数x之间线性相关,求出线性回归方程.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
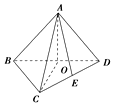 在四面体A-BCD中,AB=BC=CD=AD,∠BAD=∠BCD=90°,二面角A-BD-C为直二面角,E是CD的中点,则∠AED的度数为90°.
在四面体A-BCD中,AB=BC=CD=AD,∠BAD=∠BCD=90°,二面角A-BD-C为直二面角,E是CD的中点,则∠AED的度数为90°.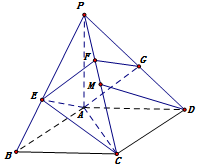 如图,PA垂直于矩形ABCD所在平面,AE⊥PB,垂足为E,EF⊥PC垂足为F.
如图,PA垂直于矩形ABCD所在平面,AE⊥PB,垂足为E,EF⊥PC垂足为F.