题目内容
数列{an}的前n项和记为Sn,已知a1=1,aa+1=
(n=1,2,3…).证明:
(Ⅰ)数列{
}是等比数列；
(Ⅱ)Sn+1=4an.
(Ⅰ) ∵an+1=Sn+1-Sn,an+1=
Sn,∴(n+2)Sn=n(Sn+1-Sn),整理得nSn+1=2(n+1)=Sn,所以
=2故{}是以2为公比的等比数列.
(Ⅱ)由(Ⅰ)知=4·
(n2).于是Sn+1=4(n+1)·=4an(n≥2).又a2=3S1=3, 故S1=a1+a2=4.因此对于任意整数n≥1,都有Sn+1=4an.
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
是函数
的一个零点.若
，则 ( )
B．
D．
，和L2=2x，其中x为销售量(单位：辆)．若该公司在这两地共销售15辆车，则能获得的最大利润为 ( )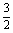
，公差d=1，求满足Sk2=(Sk)2的正整数k;
,…,akn,…成等比数列,求数列{kn}的通项kn.
且an=f(n)+f(n+1)，那么a1+a2+a3+…+a200= . 
平面
，四边形
是正方形，四边形
，
是
的中点，则
与平面
所成角的正弦值为___________。
，
，若直线
与圆
相切，则
的取值范围是（ ）
B．
D．