题目内容
已知函数f(n)= 且an=f(n)+f(n+1),那么a1+a2+a3+…+a200= .
且an=f(n)+f(n+1),那么a1+a2+a3+…+a200= .
200
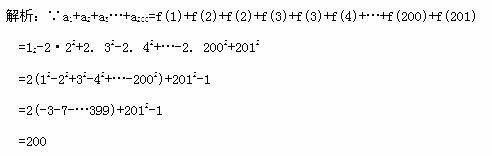

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
题目内容
已知函数f(n)= 且an=f(n)+f(n+1),那么a1+a2+a3+…+a200= .
且an=f(n)+f(n+1),那么a1+a2+a3+…+a200= .
200
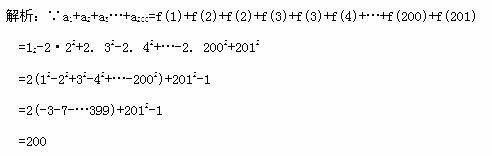

 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案