题目内容
设全集为U=R,P={x|f(x)=0},Q={x|g(x)=0},H={x|h(x)=0},则方程
=0的解集为
| f2(x)+g2(x) | h(x) |
P∩Q∩CUH
P∩Q∩CUH
.(用集合运算符号表示)分析:由已知中方程
=0,根据实数的性质,我们可得方程
=0的解集为{x|f(x)=0且g(x)=0,且h(x)≠0},进而根据P={x|f(x)=0},Q={x|g(x)=0},H={x|h(x)=0},结合集合交集的意义,得到答案.
| f2(x)+g2(x) |
| h(x) |
| f2(x)+g2(x) |
| h(x) |
解答:解:若方程
=0
则f(x)=0且g(x)=0,且h(x)≠0
由P={x|f(x)=0},Q={x|g(x)=0},H={x|h(x)=0},
故方程
=0的解集P∩Q∩CUH
故答案为:P∩Q∩CUH
| f2(x)+g2(x) |
| h(x) |
则f(x)=0且g(x)=0,且h(x)≠0
由P={x|f(x)=0},Q={x|g(x)=0},H={x|h(x)=0},
故方程
| f2(x)+g2(x) |
| h(x) |
故答案为:P∩Q∩CUH
点评:本题考查的知识点是交、并、补集的混合运算,其中根据实数的性质,解方程
=0是解答本题的关键.
| f2(x)+g2(x) |
| h(x) |

练习册系列答案
相关题目
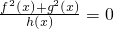 的解集为________.(用集合运算符号表示)
的解集为________.(用集合运算符号表示)