题目内容
 (2013•镇江二模)如图所示,有两条道路OM与ON,∠MON=60°,现要铺设三条下水管道OA,OB,AB(其中A,B分别在OM,ON上),若下水管道的总长度为3km,设OA=a(km),OB=b(km).
(2013•镇江二模)如图所示,有两条道路OM与ON,∠MON=60°,现要铺设三条下水管道OA,OB,AB(其中A,B分别在OM,ON上),若下水管道的总长度为3km,设OA=a(km),OB=b(km).(1)求b关于a的函数表达式,并指出a的取值范围;
(2)已知点P处有一个污水总管的接口,点P到OM的距离PH为
| ||
| 4 |
| ||
| 4 |
分析:(1)把AB的长度用含有a,b的代数式表示,在三角形AOB中利用余弦定理得到b和a的关系,即得到b关于a的函数表达式,利用三角形两边之和大于第三边得到a的取值范围;
(2)利用解析法,以O为原点,OM所在直线为x轴,建立直角坐标系,求出P点的坐标,假设AB过点P,设出A,B的坐标,写出A,B所在直线方程,把P点坐标代入直线方程求出a的值,在定义域当中,则假设成立,否则,不成立.
(2)利用解析法,以O为原点,OM所在直线为x轴,建立直角坐标系,求出P点的坐标,假设AB过点P,设出A,B的坐标,写出A,B所在直线方程,把P点坐标代入直线方程求出a的值,在定义域当中,则假设成立,否则,不成立.
解答:解:(1)∵OA+OB+AB=3,∴AB=3-a-b.
∵∠MON=60°,由余弦定理,得AB2=a2+b2-2abcos60°.
∴(3-a-b)2=a2+b2+ab.
整理,得b=
.
由a>0,b>0,3-a-b>0,及
a+b>3-a-b,a+3-a-b>b,b+3-a-b>a,得0<a<
.
综上,b=
,0<a<
.
(2)以O为原点,OM所在直线为x轴,建立如图所示直角坐标系.
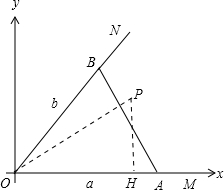
∵PH=
,PO=
,∴点P(
,
).
假设AB过点P.
∵A(a,0),B(
b,
b),即B(
•
,
•
),
∴直线AP方程为y=
(x-a),即y=
(x-a).
将点B代入,得
•
=
(
•
-a).
化简,得6a2-10a+3=0.
∴a=
.
a=
∈(0,
).
答:下水管道AB能经过污水总管的接口点P,a=
(km).
∵∠MON=60°,由余弦定理,得AB2=a2+b2-2abcos60°.
∴(3-a-b)2=a2+b2+ab.
整理,得b=
| 2a-3 |
| a-2 |
由a>0,b>0,3-a-b>0,及
a+b>3-a-b,a+3-a-b>b,b+3-a-b>a,得0<a<
| 3 |
| 2 |
综上,b=
| 2a-3 |
| a-2 |
| 3 |
| 2 |
(2)以O为原点,OM所在直线为x轴,建立如图所示直角坐标系.

∵PH=
| ||
| 4 |
| ||
| 4 |
| 1 |
| 2 |
| ||
| 4 |
假设AB过点P.
∵A(a,0),B(
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 2a-3 |
| a-2 |
| ||
| 2 |
| 2a-3 |
| a-2 |
∴直线AP方程为y=
| ||||
|
| ||
| 2-4a |
将点B代入,得
| ||
| 2 |
| 2a-3 |
| a-2 |
| ||
| 2-4a |
| 1 |
| 2 |
| 2a-3 |
| a-2 |
化简,得6a2-10a+3=0.
∴a=
5±
| ||
| 6 |
a=
5±
| ||
| 6 |
| 3 |
| 2 |
答:下水管道AB能经过污水总管的接口点P,a=
5±
| ||
| 6 |
点评:本题考查了根据实际问题选择函数模型,考查了余弦定理在解三角形中的应用,注意实际问题要有实际意义,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•镇江二模)如图,设A,B分别为椭圆
(2013•镇江二模)如图,设A,B分别为椭圆