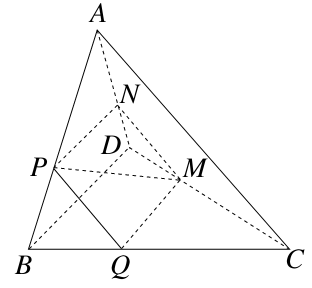
题目内容
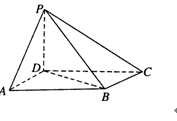
如图,四棱锥 中,底面
中,底面 为平行四边形,
为平行四边形,
 底面
底面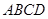
(1)证明:平面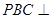 平面
平面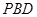 ;
;
(2)若二面角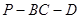 大小为
大小为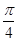 ,求
,求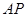 与平面
与平面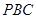 所成角的正弦值.
所成角的正弦值.
 中,底面
中,底面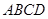 为平行四边形,
为平行四边形,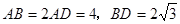
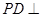 底面
底面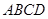
(1)证明:平面
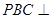 平面
平面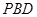 ;
;(2)若二面角
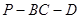 大小为
大小为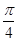 ,求
,求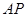 与平面
与平面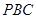 所成角的正弦值.
所成角的正弦值.
(1)详见解析;(2) .
.
 .
.试题分析:(1)根据所给数值,满足勾股定理,所以,
 ,又根据
,又根据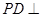 底面
底面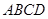 ,易证
,易证 ,所以
,所以 面
面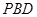 ,然后根据面面垂直的判定定理,
,然后根据面面垂直的判定定理, 面
面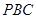 ,即证两面垂直;
,即证两面垂直;(2) ∠
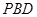 即为二面角
即为二面角 的平面角,即∠
的平面角,即∠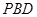
 根据已知
根据已知 两两垂直,所以可以以
两两垂直,所以可以以 为原点,如图建立空间直角坐标系,设平面
为原点,如图建立空间直角坐标系,设平面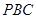 的法向量为
的法向量为 ,利用公式
,利用公式
(1)∵
 ∴
∴
又∵
 ⊥底面
⊥底面 ∴
∴
又∵
 ∴
∴ 平面
平面
而
 平面
平面 ∴平面
∴平面 平面
平面 4分
4分
(2)由(1)所证,
 平面
平面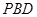 ,所以∠
,所以∠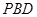 即为二面角
即为二面角 的平面角,即∠
的平面角,即∠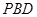

而
 ,所以
,所以
因为底面
 为平行四边形,所以
为平行四边形,所以 ,
,分别以
 、
、 、
、 为
为 轴、
轴、 轴、
轴、 轴建立空间直角坐标系.
轴建立空间直角坐标系.则
 ,
, ,
, ,
,  ,
,所以,
 ,
, ,
, ,
,设平面
 的法向量为
的法向量为 ,则
,则 即
即
令
 则
则
∴
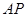 与平面
与平面 所成角的正弦值为
所成角的正弦值为 12分
12分
练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 ⊥底面
⊥底面  ,
,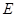 是
是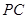 的中点,作
的中点,作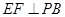 交
交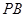 于点
于点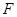 .
.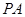
 平面
平面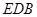 ;
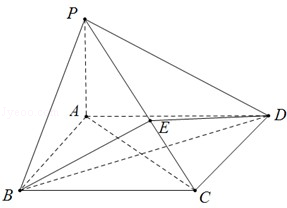
;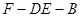 的正弦值.
的正弦值. 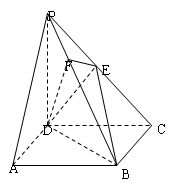
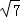 ,PA=
,PA=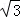 ,∠ABC=120°,G为线段PC上的点.
,∠ABC=120°,G为线段PC上的点.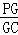 的值.
的值.
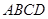 中,
中,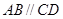 ,
,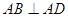 ,且
,且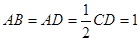 .
.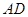 为一边向梯形外作正方形
为一边向梯形外作正方形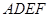 ,然后沿边
,然后沿边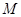 为
为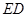 的中点,如图2.
的中点,如图2.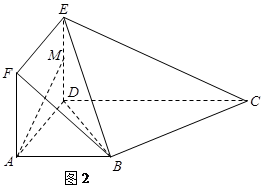
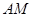 ∥平面
∥平面 ;
;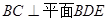 ;
;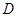 到平面
到平面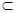 α,n∥α,则m∥n
α,n∥α,则m∥n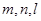 和两个不重合的平面
和两个不重合的平面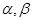 ,下列命题正确的是( )
,下列命题正确的是( )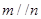 ,
,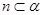 ,则
,则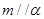
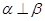 ,
,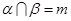 ,且
,且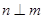 ,则
,则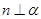
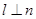 ,
,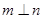 ,则
,则
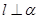 ,
,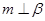 ,且
,且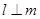 ,则
,则