题目内容
【题目】对于函数y=f(x),x∈D,若存在闭区间[a,b]![]() 和常数C,使得对任意x∈[a,b]都有f(x)=C,称f(x)为“桥函数”.
和常数C,使得对任意x∈[a,b]都有f(x)=C,称f(x)为“桥函数”.
(1)作出函数![]() 的图象,并说明f(x)是否为“桥函数”?(不必证明)
的图象,并说明f(x)是否为“桥函数”?(不必证明)
(2)设f(x)定义域为R,判断“f(x)为奇函数”是“![]() 为’桥函数’”的什么条件?给出你的结论并说明理由;
为’桥函数’”的什么条件?给出你的结论并说明理由;
(3)若函数![]() 是“桥函数”,求常数m、n的值.
是“桥函数”,求常数m、n的值.
【答案】(1)图象见解析,f(x)为“桥函数”;(2)充分不必要(3)![]() 或
或![]()
【解析】
(1)根据绝对值定义化简函数,再作图,最后根据“桥函数”定义进行判断;
(2)根据“桥函数”定义说明充分性成立,举反例说明必要性不成立;
(3)根据“桥函数”定义列等式,再根据恒成立解m、n的值.
(1)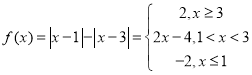
图象为
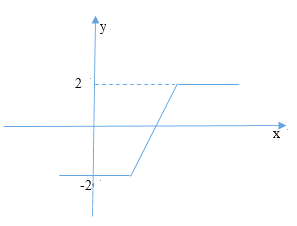
存在闭区间[3,4]![]() 和常数2,使得对任意x∈[3,4]都有f(x)=2,所以f(x)为“桥函数”
和常数2,使得对任意x∈[3,4]都有f(x)=2,所以f(x)为“桥函数”
(2)f(x)为R上奇函数,则![]() ,即存在闭区间[3,4]
,即存在闭区间[3,4]![]() 和常数0,使得对任意x∈[3,4]都有f(x)=0,所以
和常数0,使得对任意x∈[3,4]都有f(x)=0,所以![]() 为“桥函数”,
为“桥函数”,
![]() 为“桥函数”时f(x)不一定为奇函数,如
为“桥函数”时f(x)不一定为奇函数,如![]()
因此“f(x)为奇函数”是“![]() 为’桥函数’”的充分不必要条件
为’桥函数’”的充分不必要条件
(3)因为![]() 是“桥函数”,
是“桥函数”,
所以存在闭区间[a,b]![]() 和常数C,使得对任意x∈[a,b]都有g(x)=C,
和常数C,使得对任意x∈[a,b]都有g(x)=C,
即![]() ,即
,即![]()
所以![]()
即 或
或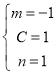 ,
,![]() 或
或![]()

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
【题目】某教师为了分析所任教班级某次考试的成绩,将全班同学的成绩作成统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
[50,60) | 3 | 0.06 |
[60,70) | m | 0.10 |
[70,80) | 13 | n |
[80,90) | p | q |
[90,100] | 9 | 0.18 |
总计 | t | 1 |
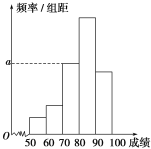
(1)求表中t,q及图中a的值;
(2)该教师从这次考试成绩低于70分的学生中随机抽取3人进行谈话,设X表示所抽取学生中成绩低于60分的人数,求随机变量X的分布列和数学期望.