题目内容
已知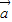
=（cosx，sinx），
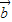=（cosβ，sinβ）（1）求证：（
）⊥（
-
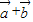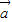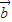）；（2）若|k
|=
|
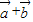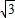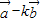|，（k＞0），将
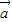与
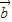数量积表示为关于k的函数f（k）；（3）求f（k）的最小值及相应
，
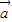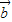夹角θ
【答案】分析：（1）直接代入数量积公式计算，求得数量积为0即可得到答案；
（2）把给出的等式两边去平方运算，展开后即可得到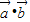
；
（3）利用基本不等式求出f（k）的最小值，由向量的夹角公式求得答案．
解答：（1）证明：∵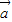
=（cosx，sinx），
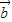=（cosβ，sinβ）
∴（
）•（
-
）=
．
∴（
）⊥（
-
）；
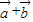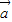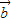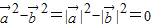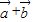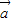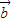（2）解：∵|k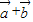
|=
|
|，∴
∴
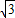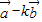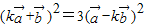
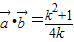，故f（k）=
；
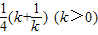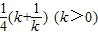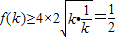（3）由f（k）=
，
∴
，当k=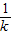
，即k=1时，取等号，此时，
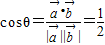，又∵0≤θ≤π，∴
．
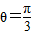点评：本题考查了数量积判断两个向量的垂直关系，考查了平面向量的坐标运算，训练了利用基本不等式求最值，考查了平面向量的夹角公式，是中档题．
（2）把给出的等式两边去平方运算，展开后即可得到
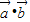；（3）利用基本不等式求出f（k）的最小值，由向量的夹角公式求得答案．
解答：（1）证明：∵
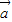=（cosx，sinx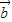），=（cosβ，sinβ）∴（
）•（-）=．∴（
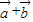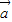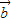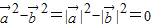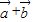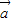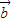）⊥（-）；（2）解：∵|k
|=||，∴∴
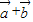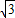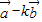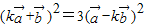
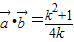，故f（k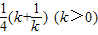）=；（3）由f（k）=
，∴
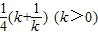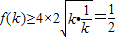，当k=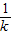，即k=1时，取等号，此时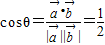，，又∵0≤θ≤π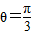，∴．点评：本题考查了数量积判断两个向量的垂直关系，考查了平面向量的坐标运算，训练了利用基本不等式求最值，考查了平面向量的夹角公式，是中档题．
练习册系列答案
相关题目
=（
cosx+
sinx，cosx），
=（cosx-sinx，2sinx），f（x）=
•
．
，b=2c，a=2
，求S△ABC．
cosx+
sinx，cosx），β=（cosx-sinx，2sinx），f（x）= α·β。
，b=2c，a=2
，求S△ABC。