题目内容
设函数
(1)求不等式 的解集;
的解集;
(2)若关于 的不等式
的不等式 在
在 上无解,求实数
上无解,求实数 的取值范围
的取值范围
(1)解集为 ;(2)
;(2) 或
或
解析试题分析:(1)该函数实质上是如下的一个分段函数, ,
,
所以原不等式转化为 或
或 或
或 ,求出每个不等式的解,然后取并集即可
,求出每个不等式的解,然后取并集即可
(2)关于 的不等式
的不等式 在
在 上无解,则
上无解,则 由上问可知函数在[0,1]单调递增,因此只要
由上问可知函数在[0,1]单调递增,因此只要 ,解此不等式即可
,解此不等式即可
试题解析:(1) ,
,
所以原不等式转化为 或
或 或
或 3分
3分
解得 ,所以原不等式的解集为
,所以原不等式的解集为 6分
6分
(2)由上问可知函数在[0,1]单调递增,因此只要 ,8分
,8分
解得 或
或 10分
10分
考点:不等式及其应用

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 ,n∈N+.
,n∈N+. ·
· .
. .
.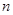 个图形中有
个图形中有 .
.
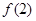 ,
, ,
, ,
, ;
; 的关系,并求出
的关系,并求出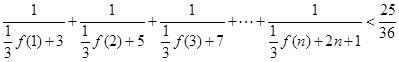 (
(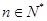 ).
). 为非负实数,满足
为非负实数,满足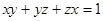 ,证明:
,证明: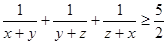 .
. 满足
满足

 的最小值.
的最小值. (x>-1)的值域.
(x>-1)的值域.