题目内容
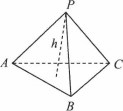
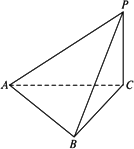
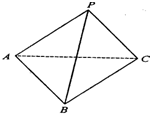 如图,四面体P-ABC中,PA=PB=PC=2,∠APB=∠BPC=∠APC=30°.一只蚂蚁从A点出发沿四面体的表面绕一周,再回到A点,问蚂蚁经过的最短路程是________.
如图,四面体P-ABC中,PA=PB=PC=2,∠APB=∠BPC=∠APC=30°.一只蚂蚁从A点出发沿四面体的表面绕一周,再回到A点,问蚂蚁经过的最短路程是________.
2
分析:将四面体P-ABC的侧面沿PA剪下再展开,得五边形PABCA'如图,可得∠A'PA=90°,且A、A'的距离等于2 ,再将此展开图围成四面体P-ABC的侧面,得到折线AD-DE-EA,得线段AD、DE、EA的和即为蚂蚁从A点出发回到A点的最短路程.
,再将此展开图围成四面体P-ABC的侧面,得到折线AD-DE-EA,得线段AD、DE、EA的和即为蚂蚁从A点出发回到A点的最短路程.
解答:将四面体P-ABC的侧面沿PA剪下再展开,得到如图所示五边形(左图)
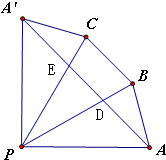
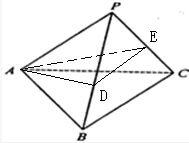
∵四面体P-ABC中,PA=PB=PC=2,∠APB=∠BPC=∠APC=30°
∴展开图中∠A'PA=3×30°=90°
连接AA',得Rt△AA'P中,AA'=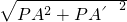 =2
=2
再将此展开图围成四面体P-ABC的侧面,得到折线AD-DE-EA
∵AA'=AD+DE+EA,
∴蚂蚁从A点出发,沿AD-DE-EA的路线行走,可得回到A点的最短路程
因此,蚂蚁从A点出发,回到A点的最短路程为2
故答案为:2
点评:本题给出四面体,求蚂蚁从侧面走一周回到出发点所走的最短路程,着重考查了解三角形和用侧面展开法求多面体表面上的最短距离问题的知识,属于中档题.

分析:将四面体P-ABC的侧面沿PA剪下再展开,得五边形PABCA'如图,可得∠A'PA=90°,且A、A'的距离等于2
 ,再将此展开图围成四面体P-ABC的侧面,得到折线AD-DE-EA,得线段AD、DE、EA的和即为蚂蚁从A点出发回到A点的最短路程.
,再将此展开图围成四面体P-ABC的侧面,得到折线AD-DE-EA,得线段AD、DE、EA的和即为蚂蚁从A点出发回到A点的最短路程.解答:将四面体P-ABC的侧面沿PA剪下再展开,得到如图所示五边形(左图)


∵四面体P-ABC中,PA=PB=PC=2,∠APB=∠BPC=∠APC=30°
∴展开图中∠A'PA=3×30°=90°
连接AA',得Rt△AA'P中,AA'=
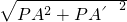 =2
=2
再将此展开图围成四面体P-ABC的侧面,得到折线AD-DE-EA
∵AA'=AD+DE+EA,
∴蚂蚁从A点出发,沿AD-DE-EA的路线行走,可得回到A点的最短路程
因此,蚂蚁从A点出发,回到A点的最短路程为2

故答案为:2

点评:本题给出四面体,求蚂蚁从侧面走一周回到出发点所走的最短路程,着重考查了解三角形和用侧面展开法求多面体表面上的最短距离问题的知识,属于中档题.

练习册系列答案
相关题目