题目内容
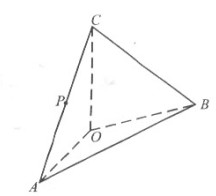
如图, 在四面体ABOC中，OC⊥OA, OC⊥OB,∠AOB=120°，且OA=OB=OC=1.(Ⅰ) 设P为AC的中点.证明：在AB上存在一点Q,使PQ⊥OA,并计算=
的值；(Ⅱ) 求二面角O-AC-B的平面角的余弦值.
II）记平面ABC的法向量为
，则由
且
，
得
故可取
又平面OAC的法向量为
练习册系列答案
相关题目
题目内容
如图, 在四面体ABOC中，OC⊥OA, OC⊥OB,∠AOB=120°，且OA=OB=OC=1.(Ⅰ) 设P为AC的中点.证明：在AB上存在一点Q,使PQ⊥OA,并计算=的值；(Ⅱ) 求二面角O-AC-B的平面角的余弦值.
II）记平面ABC的法向量为，则由
且，
得故可取
又平面OAC的法向量为
在Rt△ABC中，CA⊥CB，斜边AB上的高为h1，则
（2012•商丘三模）如图，在四面体ABCD中，CB=CD，AD⊥BD，点E，F分别是AB，BD的中点．
如图，在四面体ABOC中，OC⊥OA，OC⊥OB，∠AOB=120°，且OA=OB=OC=1
（2009•武汉模拟）如图，在四面体A-BCD中，
如图，在四面体ABOC中，OC⊥OA，OC⊥OB，∠AOB=120°，且OA=OB=OC=1．