Question

如图，四面体P-ABC，PA、PB、PC两两垂直，PA=PB=2，PC=4，E是AB的中点，F是CE的中点.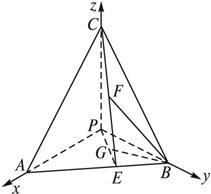

(1)写出点B、C、E、F的坐标；

(2)求BF与底面ABP所成的角的余弦值.

Answer 1

解：(1)如图, 以PA为x轴, PB为y轴, PC为z轴, P为原点建立直角坐标系, 则B点坐标为(0, 2, 0), C点坐标为(0, 0, 4), A点坐标为(2, 0, 0).

∵E为AB中点,

∴E(1, 1, 0).

∵F为CE中点,

∴F(,, 2).

(2)设G为PE中点, 则G(,, 0).

∵PA、PB、PC两两互相垂直,

∴PC⊥面ABP.

∵F、G分别为CE、PE中点,

∴FG∥PC.

∴FG⊥面ABP.

故∠FBG为BF与面ABP所成的角.

∴, , .

∴.