题目内容
【题目】已知f(x)=ax2(a∈R),g(x)=2ln x.
(1)讨论函数F(x)=f(x)-g(x)的单调性;
(2)若方程f(x)=g(x)在区间[![]() ,e]上有两个不等解,求a的取值范围.
,e]上有两个不等解,求a的取值范围.
【答案】(1)讨论见解析;(2)![]() ≤a<
≤a<![]()
【解析】
(1)首先求函数的导数![]() ,分
,分![]() 和
和![]() 两种情况讨论函数的单调性;
两种情况讨论函数的单调性;
(2)由(1)知![]() 的单调性,若满足条件,可知
的单调性,若满足条件,可知![]() 且
且![]() ,
,![]() ,
,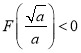 ,求得
,求得![]() 的取值范围.
的取值范围.
![]() ,
,![]() ,
,
![]() ,
,
当![]() 时,
时,![]() 恒成立,所以函数的单调递减区间是
恒成立,所以函数的单调递减区间是![]() ,
,
当![]() 时,
时,![]() 时,
时,![]() (舍)或
(舍)或![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以函数的单调递减区间是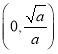 ,函数的单调递增区间是
,函数的单调递增区间是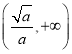 ,
,
综上可知:当![]() 时,函数的单调递减区间是
时,函数的单调递减区间是![]() ,无增区间,
,无增区间,
当![]() 时,函数的单调递减区间是
时,函数的单调递减区间是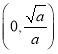 ,函数的单调递增区间是
,函数的单调递增区间是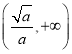 .
.
(2)即![]() 在
在![]() 上有两个不同的零点,
上有两个不同的零点,
由(1)可知![]() ,并且
,并且![]() ,
,
![]() ,
,![]() ,
,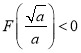 ,
,
即 ,解得:
,解得: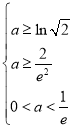 ,
,
解得:![]() ,
,
即![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目