题目内容
4.已知△ABC的面积为$\frac{\sqrt{3}}{4}$(a2+c2-b2),则sinB=$\frac{\sqrt{3}}{2}$.分析 由题意及其余弦定理可得:$\frac{1}{2}acsinB$=$\frac{\sqrt{3}}{4}$(a2+c2-b2)=$\frac{\sqrt{3}}{4}$×2accosB,化简即可得出.
解答 解:在△ABC中,由题意可得:$\frac{1}{2}acsinB$=$\frac{\sqrt{3}}{4}$(a2+c2-b2)=$\frac{\sqrt{3}}{4}$×2accosB,
∴tanB=$\sqrt{3}$,B∈(0,π),
∴B=$\frac{π}{3}$,
则sinB=$\frac{\sqrt{3}}{2}$.
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题考查了余弦定理、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.在平面直角坐标系内,以原点O为顶点,x轴非负半轴为始边,任作一角,该角的终边OA落在第一象限的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
 如图,在等腰直角三角形ABC,∠C=90°,点D在线段AB上,且AD=$\frac{1}{3}$AB,延长线段CD至点E,使DE=CD,求cos∠CBE.
如图,在等腰直角三角形ABC,∠C=90°,点D在线段AB上,且AD=$\frac{1}{3}$AB,延长线段CD至点E,使DE=CD,求cos∠CBE.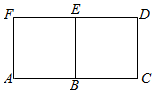 如图,矩形ACDF中,AC=2CD,B,E分别为AC,DF的中点,写出:
如图,矩形ACDF中,AC=2CD,B,E分别为AC,DF的中点,写出: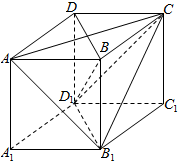 如图,棱长为1的正方体ABCD-A1B1C1D1中,
如图,棱长为1的正方体ABCD-A1B1C1D1中,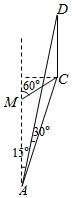 如图,为了测量河对岸电视塔CD的高度,小王在点A处测得塔顶D仰角为30°,塔底C与A的连线同河岸成15°角,小王向前走了1200m到达M处,测得塔底C与M的连线同河岸成60°角,则电视塔CD的高度为600$\sqrt{2}$m.
如图,为了测量河对岸电视塔CD的高度,小王在点A处测得塔顶D仰角为30°,塔底C与A的连线同河岸成15°角,小王向前走了1200m到达M处,测得塔底C与M的连线同河岸成60°角,则电视塔CD的高度为600$\sqrt{2}$m.