题目内容
设函数 。
。
(1)如果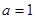 ,求函数
,求函数 的单调递减区间;
的单调递减区间;
(2)若函数 在区间
在区间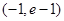 上单调递增,求实数
上单调递增,求实数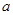 的取值范围;
的取值范围;
(3)证明:当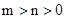 时,
时,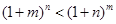
(1)函数的单调减区间为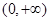 .(2)
.(2)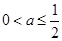 .(3)分析法
.(3)分析法
解析试题分析:首先求导数,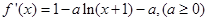
讨论得到当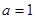 时,
时,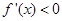 ,确定函数的单调减区间为
,确定函数的单调减区间为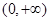 .
.
(2)注意讨论①当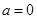 时,情况特殊;②当
时,情况特殊;②当 时,令
时,令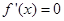 ,求驻点,讨论
,求驻点,讨论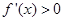 时,得函数的增区间为
时,得函数的增区间为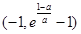 ;
;
根据函数 在区间
在区间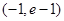 上单调递增,得到
上单调递增,得到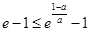 ,得出所求范围..
,得出所求范围..
(3)利用分析法,转化成证明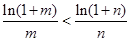 ;
;
构造函数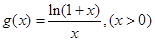 ,
,
应用导数知识求解
试题解析:(1)函数的定义域为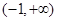 ,
,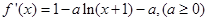
当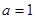 时,
时,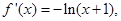
 时,
时,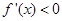 ,所以,函数的单调减区间为
,所以,函数的单调减区间为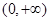 .
.
(2)①当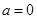 时,
时,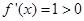 ,所以,函数的单调增区间为
,所以,函数的单调增区间为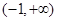 ;
;
②当 时,令
时,令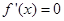 ,得
,得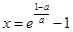 ,
,
当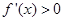 时,得
时,得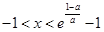 ,函数的增区间为
,函数的增区间为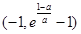 ;
;
又因为,函数 在区间
在区间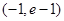 上单调递增,
上单调递增,
所以,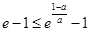 ,得
,得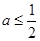 ,综上知,
,综上知,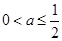 .
.
(3)要证: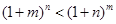 只需证
只需证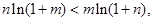
只需证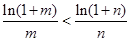
设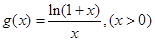 ,
,
则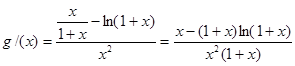 11分
11分
由(1)知:即当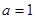 时,
时,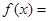
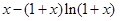 在
在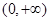 单调递减,
单调递减,
即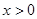 时,有
时,有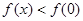 , 12分
, 12分
∴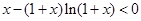 ,所以
,所以
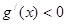 ,即
,即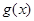 是
是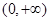 上的减函数, 13分
上的减函数, 13分
即当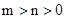 ,∴
,∴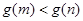 ,故原不等式成立。 14分
,故原不等式成立。 14分
考点:应用导数研究函数的单调性、证明不等式.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
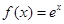 (
(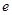 为自然对数的底数),
为自然对数的底数),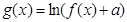 (
(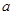 为常数),
为常数),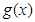 是实数集
是实数集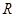 上的奇函数.
上的奇函数.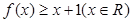 ;
; 的方程:
的方程: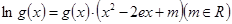 的根的个数;
的根的个数;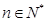 ,证明:
,证明: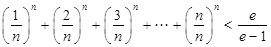 (
(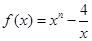 ,且
,且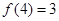 .
.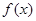 的奇偶性并说明理由;
的奇偶性并说明理由;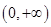 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;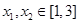 ,有
,有 成立,求
成立,求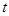 的最小值.
的最小值.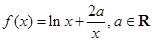 .
. 在
在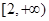 上是增函数,求实数
上是增函数,求实数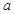 的取值范围;
的取值范围; 上的最小值为3,求实数
上的最小值为3,求实数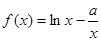 (
(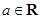 ).
).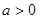 时,判断
时,判断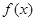 在定义域上的单调性;
在定义域上的单调性;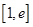 上的最小值为
上的最小值为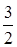 ,求
,求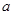 的值;
的值;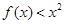 在
在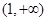 上恒成立,试求
上恒成立,试求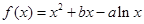
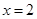 是函数
是函数 的极值点,
的极值点,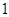 和
和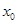 是函数
是函数 ,求
,求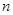 ;
;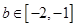 ,都存在
,都存在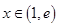 (
(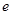 为自然对数的底数),使得
为自然对数的底数),使得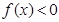 成立,求实数
成立,求实数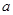 的取值范围.
的取值范围.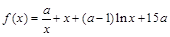 ,
,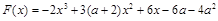 ,其中
,其中 且
且 .
.  ,求函数
,求函数 的单调递增区间;
的单调递增区间; 时,函数
时,函数 有极值,求函数
有极值,求函数 (
( 是自然对数的底数),是否存在a使
是自然对数的底数),是否存在a使 在
在 上为减函数,若存在,求实数a的范围;若不存在,请说明理由.
上为减函数,若存在,求实数a的范围;若不存在,请说明理由.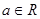 ,函数
,函数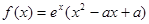 .
.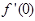 的值;
的值; 的单调区间.
的单调区间.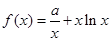 ,
,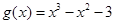 .
.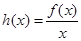 的单调性;
的单调性;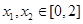 ,使得
,使得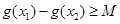 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数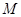 ;
;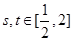 ,都有
,都有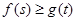 成立,求实数
成立,求实数 的取值范围.
的取值范围.