题目内容
设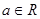 ,函数
,函数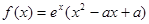 .
.
(Ⅰ)求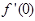 的值;
的值;
(Ⅱ)求函数 的单调区间.
的单调区间.
(Ⅰ) ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
解析试题分析:(Ⅰ)本小题首先需要对原函数求导得 ,然后代入
,然后代入 ;
;
(Ⅱ)本小题首先令 ,得
,得 ,然后分析二根之间的关系,需要分类讨论,按
,然后分析二根之间的关系,需要分类讨论,按 ;
; ;
; 进行.
进行.
试题解析:(Ⅰ)
∴ . 3分
. 3分
(Ⅱ)令 ,得
,得 4分
4分
函数 定义域为R,且对任意
定义域为R,且对任意 R,
R, ,
,
当 ,即
,即 时,
时, ,
, 的单调递增区间是
的单调递增区间是 . 6分
. 6分
当 ,即
,即 时,
时,
所以 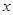

0 



+ 0 - 0 + 
↗ ↘ ↗  的单调递增区间是
的单调递增区间是 ,
, ,单调递减区间是
,单调递减区间是
练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
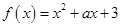 .
.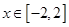 时,
时,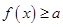 恒成立,求实数
恒成立,求实数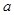 的取值范围;
的取值范围;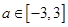 ,
,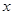 的取值范围.
的取值范围. 。
。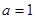 ,求函数
,求函数 的单调递减区间;
的单调递减区间;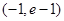 上单调递增,求实数
上单调递增,求实数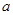 的取值范围;
的取值范围;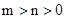 时,
时,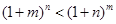
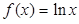 .
.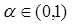 ,求
,求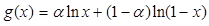 最大值;
最大值;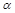 ,
,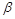 满足
满足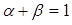 .求证:
.求证: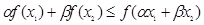 ;
;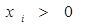 ,正数
,正数 满足
满足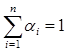 .证明:
.证明: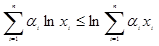
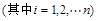 .
. +
+ ,g(x)=
,g(x)= ln(2ex)(其中e为自然对数的底数)
ln(2ex)(其中e为自然对数的底数) }中,a1=1,
}中,a1=1,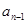 )(n≥2),求证:
)(n≥2),求证: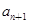 <
< <
< .
.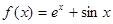 ,
,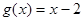 ;
;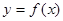 在
在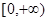 上单调递增;
上单调递增;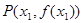 ,
,
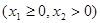 ,若直线
,若直线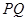
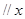 轴,求
轴,求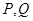 两点间的最短距离.
两点间的最短距离.  和
和 是函数
是函数 的两个极值点,其中
的两个极值点,其中 ,
, .
. 的取值范围;
的取值范围; ,求
,求 的最大值.注:e是自然对数的底.
的最大值.注:e是自然对数的底.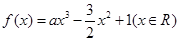 ,其中
,其中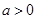 .
. ,求曲线
,求曲线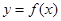 在点
在点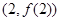 处的切线方程;
处的切线方程; 有三个零点,求
有三个零点,求 的取值范围.
的取值范围. ,
, 在
在 处切线方程;
处切线方程; 上单调递减;
上单调递减; 对任意的
对任意的 都成立,求实数
都成立,求实数 的最大值.
的最大值.