Question

若函数f（x）=log_a（x+1）（a＞0，a≠1）的定义域和值域都是[0，1]，则a等于（ ）
A．
B．
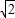
C．
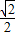
D．2

Answer 1

【答案】分析：由“f（x）=log_a（x+1）的定义域是[0，1]”，可知0≤x≤1，从而有1≤x+1≤2．再利用对数函数的单调性研究：当a＞1时，是增函数，则有0=log_a1≤log_a（x+1）≤log_a2=1；当0＜a＜1时，是减函数，则有log_a2≤log_a（x+1）≤log_a1=0，分别求解，最后取并集．
解答：解：f（x）=log_a（x+1）的定义域是[0，1]，
∴0≤x≤1，则1≤x+1≤2．
当a＞1时，0=log_a1≤log_a（x+1）≤log_a2=1，
∴a=2；
当0＜a＜1时，log_a2≤log_a（x+1）≤log_a1=0，
与值域是[0，1]矛盾．
综上，a=2．
故选D
点评：本题主要通过函数间的转化，来考查对数函数的定义域，值域及其单调性，还考查了转化和分类讨论思想．