题目内容
(本小题满分12分)已知函数¦(x)=2―sin(2x+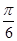 )―2sin2x,x∈[0,
)―2sin2x,x∈[0,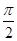 ]
]
(1)求函数¦(x)的值域;
(2)记△ABC的内角A、B、C所对的边长分别为a、b、c,若¦(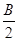 )=1,b=1,c=
)=1,b=1,c=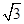 ,求a的值
,求a的值
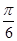 )―2sin2x,x∈[0,
)―2sin2x,x∈[0,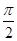 ]
](1)求函数¦(x)的值域;
(2)记△ABC的内角A、B、C所对的边长分别为a、b、c,若¦(
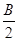 )=1,b=1,c=
)=1,b=1,c=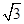 ,求a的值
,求a的值(1) (2)
(2)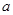 的值为1或2
的值为1或2
 (2)
(2)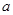 的值为1或2
的值为1或2(1)利用二倍角和两角和差的正余弦公式化简函数,然后利用函数的单调性求出函数的值域;(2)根据函数的值域求出角B,然后利用正弦定理求出角C,进一步求出边a
解:(1)
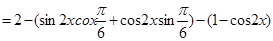
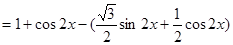
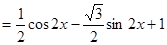
 …………………………………………………………………………4分
…………………………………………………………………………4分
 ,
, ,
, ,
,
所以函数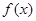 的值域是
的值域是 ;…………………………………………………………6分
;…………………………………………………………6分
(2)由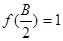 得
得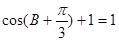 ,即
,即
又因为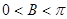 ,所以
,所以
所以 ,即
,即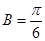 . ………………………………………………………………8分
. ………………………………………………………………8分
因为 ,所以由正弦定理
,所以由正弦定理 ,得
,得 ,故
,故
当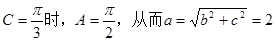
当
故 的值为1或2. …………………………………………………………………12分
的值为1或2. …………………………………………………………………12分
解:(1)

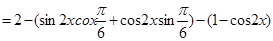
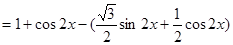
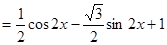
 …………………………………………………………………………4分
…………………………………………………………………………4分 ,
, ,
, ,
,所以函数
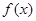 的值域是
的值域是 ;…………………………………………………………6分
;…………………………………………………………6分(2)由
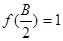 得
得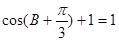 ,即
,即
又因为
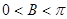 ,所以
,所以
所以
 ,即
,即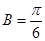 . ………………………………………………………………8分
. ………………………………………………………………8分因为
 ,所以由正弦定理
,所以由正弦定理 ,得
,得 ,故
,故
当
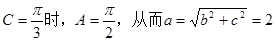
当

故
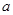 的值为1或2. …………………………………………………………………12分
的值为1或2. …………………………………………………………………12分
练习册系列答案
相关题目
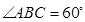 ,
,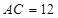 ,
,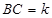 的
的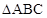 恰有一个,那么
恰有一个,那么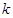 的取值范围是( )
的取值范围是( )
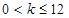
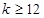
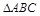 中,角
中,角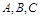 所对的边分别为
所对的边分别为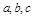 ,已知
,已知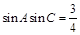 .
.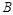 的大小;
的大小;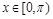 ,求函数
,求函数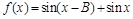 的值域.
的值域. 且与点A相距40
且与点A相距40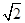 海里的位置B,经过40分钟又测得该船已行驶到点A北偏东
海里的位置B,经过40分钟又测得该船已行驶到点A北偏东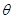 (其中sin
(其中sin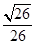 ,
, )且与点A相距10
)且与点A相距10 海里的位置C.
海里的位置C. 

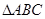 中,已知
中,已知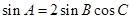 ,则
,则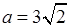 ,
,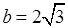 ,
,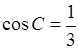 ,则
,则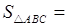 _______
_______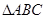 中,已知
中,已知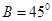 ,
,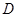 是
是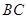 边上的一点,
边上的一点, 
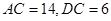 ,则
,则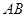 的长为 .
的长为 .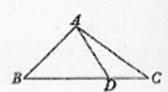
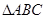 中,
中, 、
、 、
、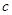 分别为内角
分别为内角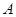 、
、 、
、 所对的边,已知
所对的边,已知 ,
, ,
, ,则
,则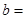 ( )
( )