题目内容
△ABC中,2A=B+C,a=2b·cosC,则三角形的形状为( )三角形
| A.直角 | B.直角等腰 | C.等腰三角形 | D.等边三角形 |
D
解:因为2A=B+C,a=2b·cosC,则A=600,则sinA=2sinBcosC
即为sinBcosC –cosBsinC="0,sin(B-C)" =0,说明了三角形一定是等边三角形,选D
即为sinBcosC –cosBsinC="0,sin(B-C)" =0,说明了三角形一定是等边三角形,选D

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
 中,内角
中,内角 的对边分别为
的对边分别为 ,若
,若 ,则
,则 的取值范围是( )
的取值范围是( )



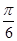 )―2sin2x,x∈[0,
)―2sin2x,x∈[0,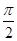 ]
]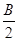 )=1,b=1,c=
)=1,b=1,c=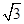 ,求a的值
,求a的值 的内角
的内角 的对边分别为
的对边分别为 ,且
,且 ,则
,则
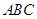 中,A,B,C。的对边分别为a,b,c,且
中,A,B,C。的对边分别为a,b,c,且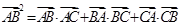
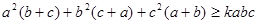 ,对任意的满足题意的a,b,c都成立,求实数k的取值范围.
,对任意的满足题意的a,b,c都成立,求实数k的取值范围. 、
、 、
、 分别是
分别是 的三个内角
的三个内角 、
、 、
、 所对的边.
所对的边. ,求
,求 的值;
的值; ,且
,且 ,试判断
,试判断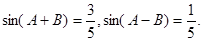 (14分)
(14分) ;
; 分别为
分别为 三个内角
三个内角 的对边,
的对边,
 (2)若
(2)若 ,
, ;求
;求 .
. 中,三边
中,三边 所对角依次为
所对角依次为 ,则
,则 _____________
_____________