题目内容

14．设z1，z2∈C，z12-4z1z2+4z22=0，|z2|=2，则以|z1|为直径的圆面积为（　　）
A．πB．4πC．8πD．16π

分析 由已知可得（z1-2z2）2=0，因此z1=2z2．再利用|z2|=2，即可得出|z1|．

解答 解：∵${{z}_{1}}^{2}$-4z1z2+4${{z}_{2}}^{2}$=0，
∴（z1-2z2）2=0，∴z1=2z2．
∴|z1|=2|z2|=4，
∴以|z1|为直径的圆的面积=π×（$\frac{4}{2}$）2=4π．
故选：B．

点评 熟练掌握复数的运算和模的意义是解题的关键．

练习册系列答案
相关题目
4．在等差数列{an}中，Sn为其前n项和，S7=35，a2+a3+a10=12，则Sn的最大值为（　　）
A．28B．36C．45D．55
5．在平面四边形ACBD（图①）中，△ABC与△ABD均为直角三角形且有公共斜边AB，设AB=2，∠BAD=30°，∠BAC=45°，将△ABC沿AB折起，构成如图②所示的三棱锥C′-ABC．
（Ⅰ）当$C'D=\sqrt{2}$时，求证：平面C′AB⊥平面DAB；①②
（Ⅱ）当AC′⊥BD时，求三棱锥C′-ABD的高．
2．已知m∈R，向量$\overrightarrow a=（m，1）$，$\overrightarrow b=（2，-6）$，且$\overrightarrow a⊥\overrightarrow b$，则$|\overrightarrow a-\overrightarrow b|$=$5\sqrt{2}$．
9．正整数a、b满足1＜a＜b，若关于x、y的方程组$\left\{\begin{array}{l}{y=-2x+4033}\\{y=|x-1|+|x+a|+|x-b|}\end{array}\right.$有且只有一组解，则a的最大值为4031．
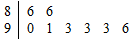19．如图是某班8位学生诗词比赛得分的茎叶图，那么这8位学生得分的众数和中位数分别为93、92．
6．已知点A（-3，2），在直线y=-x点找一点B，在x轴上找一点C，使此三点构成三角形，则△ABC的周长的最小值为$\sqrt{26}$．
3．根据函数y=f（x）的图象，求：f（0），f（3），定义域D，值域M，最值，单调减区间．
4．已知向量$\overrightarrow{m}$=（$\frac{3}{2}$，-sinx），$\overrightarrow{n}$=（1，sinx+$\sqrt{3}$cosx），x∈R，函数f（x）=$\overrightarrow{m}$•$\overrightarrow{n}$．
（I）求f（x）的最小正周期及值域；
（2）已知△ABC中，角A、B、C的对边分别为a，b，c，若f（A）=0，a=$\sqrt{3}$，bc=2，求△ABC的周长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网