题目内容
某林场原有森林木材存有量为a m3,木材以每年25%的增长率增长,而每年冬天计划要砍伐的木材量为x m3,为了实现经过20年达到木材存有量至少翻两番的目标,求x的最大值(计算时取lg2≈0.3,lg5≈0.7).
解:第1年末的木材存有量为
a-x,
第2年末的木材存有量为(
a-x)
-x=(
)2a-x(1+
),
第3年末的木材存有量为
-x［1+
+(
)2］,
…
第20年末的木材存有量为(
)20a-x［1+
+(
)2+…+(
)19］=(
)20a-4x(
)20+4x.
由题意知(
)20a-4x(
)20+4x≥4a.
令y=(
)20,则lgy=20(lg5-lg4)=20(1-3lg2)≈2,
∴y≈100.
∴100a-400x+4x≥4a
x≤
a.
故每年砍伐量不能超过
a.
练习册系列答案
相关题目
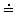0.3)